[Высшая математика] Вычислить определённый интеграл: 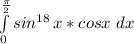
Другие вопросы по теме Математика
Популярные вопросы
- Напишите сочинение на тему каким должен быть современный мир...
2 - не пишется вместе или раздельно? (не) брежный (не) сладкий...
2 - Найдите диаметр круга, если его площадь равна: 314мм2(квадратных...
3 - Какой плод у щавеля сухой или сочный...
3 - 100% угля добывается открытым а) кузбасс б) канско-ачинский...
2 - Cos a,если sin a = - 1/2, п меньше а меньше 3п/2...
3 - Скласти розповідь про дітей на катку використовуючи займенник...
1 - Сравните площади круга и прямоугольника радиус круга 6 см длина...
2 - Как отличить что это относительное , качественное , притяжительное...
3 - Морфологический разбор: извилистую дорогу, прения-оживленные,...
1
1/19
Пошаговое объяснение:
df(x)=f'(x)*dx⇒cosx*dx=d(sinx)
введем замену sinx=t
тогда пределы интегрирования изменятся так:
нижний предел tнижн.= sin0=0; верхний tверхн.=sinπ/2=1;
∫t⁸dt=t¹⁹/19
подставим по формуле Ньютона - Лейбница пределы интегрирования. получим (1¹⁹/19)-(0¹⁹/19)=1/19
Метод замены переменной в определённом интеграле .