Высшая математика, буду благодарен! 1. Решить:
Найти точку E пересечения медиан треугольника, вершинами которого есть точки A(-3;1), B(7;5), C(5;-3);
2. Доказать, что прямые параллельны, и найти расстояние между ними: (скрин 1).
3. Составить каноническое уравнение прямой. (cкрин 2).
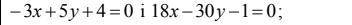
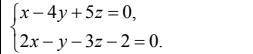
Другие вопросы по теме Математика
Популярные вопросы
- Правильно составить предложения! write the dialogue. then act it out in pairs....
3 - Сочинение по биологии я и биология 5 класс...
3 - Периметр треугольника равен 7дм 9см. первая его сторона равна34см,вторая-2дм....
1 - Выписать слова в которых есть непарные по звонкости, глухости согласные. таня...
2 - Что оригинального нарисовать на олимпийские игры?...
2 - Бокавая сторона равнобедренного треугольника на 4 см длиннее основание,а периметр...
3 - Какие растения остаются зелеными, на каких много желтых и красных листьев?...
1 - Что обозначает пословица мир вам и я к вам...
2 - Очважно прям капец челы, проверьте ошибки в диалоге. мб еще что-нибудь допишите....
3 - Т..жёлые капли (за)барабанили (по)г..л..ве и пл..чам капитана кор..левской стражи....
2
1. Чтобы найти точку E пересечения медиан треугольника, мы должны найти сначала координаты вершин треугольника. В данном случае, вершины треугольника заданы координатами A(-3,1), B(7,5) и C(5,-3).
Чтобы найти координаты точки E, которая является пересечением медиан треугольника, нам нужно найти среднее арифметическое всех вершин треугольника.
Для этого мы сложим координаты каждой вершины и поделим на 3:
x_E = (x_A + x_B + x_C)/3
y_E = (y_A + y_B + y_C)/3
Теперь подставим значения координат вершин:
x_E = (-3 + 7 + 5)/3 = 3/3 = 1
y_E = (1 + 5 - 3)/3 = 3/3 = 1
Таким образом, координаты точки E равны (1,1).
2. Чтобы доказать, что прямые параллельны и найти расстояние между ними, воспользуемся уравнениями данных прямых.
Начнем с уравнений прямых:
а) x + 3y - 5 = 0
б) 2x + 6y - 7 = 0
Прямые будут параллельными, если их нормальные векторы пропорциональны. Нормальный вектор для прямой заданного уравнения имеет коэффициенты при x и у, обратные соответственно коэффициентам при x и у в уравнении прямой.
Поэтому, для прямой а) нормальным вектором будет (1, 3)
Для прямой б) нормальным вектором будет (2, 6)
Выполним проверку:
Если (2, 6) = k * (1, 3), где k - некоторая константа, то прямые параллельны.
Сравнивая соответствующие координаты, мы видим, что каждая компонента вектора (2, 6) является удвоенной компонентой вектора (1, 3). Это означает, что k = 2.
Следовательно, прямые а) и б) параллельны.
Мы можем найти расстояние между параллельными прямыми, используя следующую формулу:
d = |c_2 - c_1| / sqrt(a_1^2 + b_1^2)
Где a_1, b_1 - коэффициенты при x и y в уравнении прямой а), а c_1 - свободный член уравнения прямой а).
a_2, b_2 - коэффициенты при x и y в уравнении прямой б), а c_2 - свободный член уравнения прямой б).
Подставим значения для прямых а) и б):
a_1 = 1, b_1 = 3, c_1 = -5
a_2 = 2, b_2 = 6, c_2 = -7
Теперь вычислим расстояние:
d = |(-7) - (-5)| / sqrt(1^2 + 3^2) = |-2| / sqrt(1 + 9) = 2 / sqrt(10)
Таким образом, расстояние между прямыми а) и б) равно 2 / sqrt(10).
3. Чтобы составить каноническое уравнение прямой, нужно знать ее наклон и координаты одной точки на прямой.
На скриншоте не указаны координаты и/или наклон прямой, поэтому я не могу составить каноническое уравнение прямой на основе этой информации. Если вы предоставите дополнительные данные, я смогу помочь вам с этой задачей.
Надеюсь, что эти объяснения помогли! Если у вас возникнут еще вопросы, не стесняйтесь задавать.