Высш. мат. Установить, какая линия определяется уравнением, нарисовать её.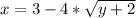
Другие вопросы по теме Математика
Популярные вопросы
- Альтруистский взгляд на мир определение...
2 - Ребят , кому не сложно) Векторы. 582; 583(б) , по рисунку 127...
3 - Объясните слова и словосочетания:скудный, пронзил, точка, блеснёт, испуганные...
2 - Айтылымтапсырма.«Жағдаят: Бүгін - сенбі. Досың екеуі.келесі аптада сабақтан...
2 - Определи вес стального кубика с ребром длиной 25 см. (Ускорение свободного...
1 - в однорідному магнітному полі з індукцією 0.1 тл рівномірно обертається...
1 - Почему для программистов 6.99 это 8?...
2 - 2ax=6x Чему равен а? x^2-2ax+a^2 x^2-6x+......
2 - До ть записати складносурядні речення, самостійно дібравши спільний для...
3 - Найдите метафору в приведенном предложении и объясните ее значение: Во всём...
3
Уравнение, данное в задаче, является уравнением прямой в координатной плоскости.
Давайте начнем с разрешения уравнения относительно переменной x. Для этого нам нужно избавиться от корня в выражении 4*√(y+2). Для этого возводим обе части уравнения в квадрат:
(x + 4*sqrt(y + 2))^2 = (3-4*sqrt(y+2))^2
Раскроем квадрат на обеих сторонах уравнения:
x^2 + 8*x*sqrt(y+2) + 16(y+2) = 9 - 6*sqrt(y+2) + 16(y+2)
Упростим выражение, объединим подобные члены:
x^2 + 8*x*sqrt(y+2) + 16y + 32 = 9 - 6*sqrt(y+2) + 16y + 32
x^2 + 8*x*sqrt(y+2) - 6*sqrt(y+2) = 9
Выделим корень sqrt(y+2) в выражении:
(sqrt(y + 2))^2*(x^2 + 8*x - 6) = 9
(y + 2)*(x^2 + 8*x - 6) = 9
(x^2 + 8*x - 6)*(y + 2) = 9
Теперь у нас есть уравнение, связывающее переменные x и y. Заметим, что x и y являются координатами точек на плоскости. После раскрытия скобок, получим уравнение квадратного многочлена:
x^2*y + 8*x*y + 2*x^2 + 16*y + 4*x - 12 = 9
Это уравнение не представляется в явном виде прямой, однако мы можем нарисовать график этой функции, чтобы лучше понять ее форму и характеристики.
Чтобы построить график этой линии, мы можем использовать метод подстановки точек и построить таблицу значений. Выбираем различные значения для x и подставляем их в уравнение, чтобы найти соответствующие значения y.
Допустим, мы выбираем несколько значений для x: -2, -1, 0, 1 и 2. Подставляем их в уравнение и находим соответствующие значения y.
Подставим x = -2:
(-2)^2*y + 8*(-2)*y + 2*(-2)^2 + 16*y + 4*(-2) - 12 = 9
4y - 16y - 8 + 16y - 8 - 12 = 9
-12 = 9 (Уравнение не выполняется, нет решений)
Подставим x = -1:
(-1)^2*y + 8*(-1)*y + 2*(-1)^2 + 16*y + 4*(-1) - 12 = 9
y - 8y + 2 + 16y - 4 - 12 = 9
9y - 14 = 9
9y = 23
y = 23/9
Подставим x = 0:
0^2*y + 8*0*y + 2*0^2 + 16*y + 4*0 - 12 = 9
16y - 12 = 9
16y = 21
y = 21/16
Подставим x = 1:
1^2*y + 8*1*y + 2*1^2 + 16*y + 4*1 - 12 = 9
y + 8y + 2 + 16y + 4 - 12 = 9
25y - 6 = 9
25y = 15
y = 3/5
Подставим x = 2:
2^2*y + 8*2*y + 2*2^2 + 16*y + 4*2 - 12 = 9
4y + 16y + 8 + 16y + 8 - 12 = 9
36y + 4 = 9
36y = 5
y = 5/36
Теперь у нас есть несколько точек (x, y), которые удовлетворяют уравнению. Мы можем использовать эти точки, чтобы нарисовать график уравнения.
Построим таблицу значений:
x | y
-------
-1 | 23/9
0 | 21/16
1 | 3/5
2 | 5/36
Теперь мы можем нарисовать график, используя эти точки. Подключим эти точки и получим график.
Но для более точной и наглядной визуализации графика, лучше использовать графическую программу или калькулятор с возможностью построения графиков.