Высота правильной четырехугольной пи-
рамиды равна 8, боковое ребро - 10. Найдите площадь основания пирамиды.​

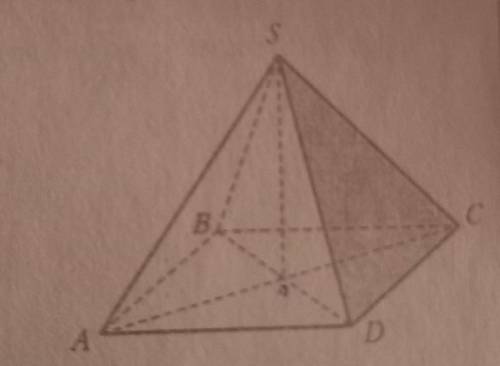
Дано : SABCD - правильная пирамида,

           SO ⊥ (ABCD),  SO = 8,

           SA = SB = SC = SD = 10

Найти :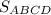

В основании правильной четырёхугольной пирамиды лежит квадрат, высота опускается в точку пересечения диагоналей квадрата.

ΔSOC :      ∠SOC = 90°;  SO = 8;  SC = 10

По теореме Пифагора

CO = 6

Диагонали квадрата равны и точкой пересечения делятся пополам

⇒   BD = AC = 2 · CO = 2 · 6 = 12

Площадь квадрата равна половине квадрата диагонали

ответ : 72 кв. ед.