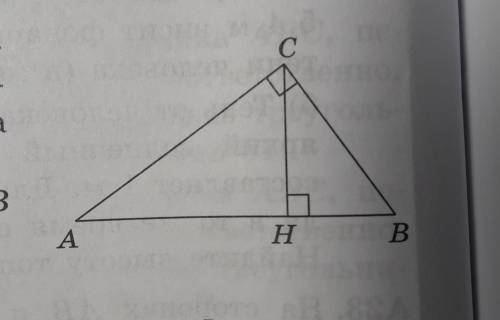
Высота CH прямоугольного треугольника ABC, проведённая к гипотенузе AB, делит треугольник на два меньших. Докажите, что треугольники AHC, CHB и ACB подобны между собой.
Другие вопросы по теме Математика
Популярные вопросы
- Решите уранение -4(- 5)–(- 30):6...
1 - ұй жұмысы xx ғасырдың басындағы Қазақстанның əлеуметтік-экономикалық...
3 - Определи, согласно тексту, значение слова «турист»...
1 - Памагите/ укажите уравнение которое не имеет корней/с решениями...
1 - 4-2(x+3)=4(x-5) Решите уравнение...
2 - Что тренирует ум человека?...
1 - Кочевое общество объединяется по -... а)родовому принципу б)политическому...
3 - Что делать чтобы получить образование? ...
3 - найти площадь и объем комнаты...
2 - Решите задачу с уравнения. Маша задумала число. Если его вычесть...
2
1. Доказательство равенства углов:
- Угол ACH является прямым углом, так как это высота прямоугольного треугольника ABC и она перпендикулярна к основанию AB.
- Угол BHC также является прямым углом, так как это высота прямоугольного треугольника ABC и она перпендикулярна к основанию AB.
- Угол ACB является прямым углом, так как это угол прямоугольного треугольника ABC с гипотенузой AB.
Таким образом, все три треугольника имеют прямые углы ACH, BHC и ACB, следовательно, углы AHC, CHB и ACB равны.
2. Доказательство равенства отношений сторон:
У нас есть два меньших треугольника: AHC и CHB. Они оба включают высоту CH, поэтому мы можем использовать теорему Пифагора, чтобы найти соотношение между их сторонами.
В треугольнике AHC:
AH^2 + CH^2 = AC^2 (теорема Пифагора)
В треугольнике CHB:
CH^2 + BH^2 = CB^2 (теорема Пифагора)
Так как CH^2 появляется в обоих уравнениях, мы можем сократить его и получить:
AH^2 = AC^2 - CH^2
BH^2 = CB^2 - CH^2
Таким образом, соотношение между сторонами треугольников AHC и CHB такое же:
AH^2 = AC^2 - CH^2 = BH^2 = CB^2 - CH^2
Также, из равенства углов AHC и CHB, мы можем сделать вывод, что соотношение между сторонами треугольников AHC и CHB также равно:
AC/AH = CH/CB
Таким образом, мы доказали, что соотношение длин сторон и равенство углов треугольников AHC, CHB и ACB одинаковы. Следовательно, эти треугольники подобны.