Выразить ) и
и ) через первые степени синусов и косинусов аргументов, кртаных
через первые степени синусов и косинусов аргументов, кртаных 
Другие вопросы по теме Математика
Популярные вопросы
- Для развития западной европейской госуд. хl-xv веках...
3 - Реши уравнения 65+(x+23)=105 (48-x)+35=82 90+y*8=154 120: (x-19)=6...
1 - Продолжи сказку жили были три брата и решили они отправиться счастье искать...
1 - Решите ситуационные 1. иванов обратился в пенсионные органы за назначением пенсии...
3 - Как прославились саул, давид и соломон...
3 - Выпишите грамматическую основу: застыв,пинчук решил заштопать дырку в гимнастерке....
2 - linda to learn italian поставить предложение во все времена...
3 - Сбез уровнения сумма двух чисел 230. если первоеииз них уменьшить на 20, то...
2 - Составьте уравнения реакций между веществами и назовите продукты реакции: а)...
3 - Почему петух и курица отличаются окрасом...
1
Будем использовать формулу Эйлера:
И по формуле бинома Ньютона
Аналогично для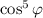 также делается как и с синусом.
также делается как и с синусом.