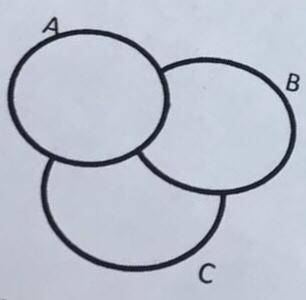
Выделите области, представляющие множество А\В⋂С
Заранее )

Для того чтобы выделить области, представляющие множество А\В⋂С, нам необходимо знать определения множеств А, В и С, их пересекающихся частей, а также операцию разности множеств А\В.

Давайте разберем каждую часть по порядку:

1. Множество А:
Здесь мы видим, что множество А состоит из двух частей: левой и правой. Левая часть ограничена вертикальной прямой и граничит с множеством С. Правая часть ограничена вертикальной прямой и граничит с множеством В.

2. Множество В:
Множество В представлено в виде горизонтальной прямой, ограниченной сверху и снизу границами множества А.

3. Множество С:
Множество С также представлено в виде горизонтальной прямой, ограниченной сверху и снизу границами множества А, но смещено по горизонтали вправо.

4. Множество А\В:
Операция разности множеств А\В означает, что мы должны удалить из множества А элементы, принадлежащие множеству В.

Теперь мы можем приступить к выделению областей, представляющих множество А\В⋂С.

1. Начинать будем с самого верхнего края диаграммы. Здесь мы видим горизонтальную линию, обозначающую границу множества В.

2. Переходим к множеству А. В нем есть две части (левая и правая), но для определения областей А\В⋂С будем рассматривать только ту часть множества, которая находится выше горизонтальной линии, обозначающей границу множества В. Поскольку множество С смещено вправо, его граница пересекает часть множества А, ограниченную вертикальной прямой. Эта часть множества А, пересекающаяся с множеством С, и составляет первую область.

3. Полученная первая область представляет собой треугольник, который образуется пересечением границ множества А и границ множества С. Часть этого треугольника нужно выделить именно как область А\В⋂С.

4. Поскольку нам нужно рассмотреть только области, представляющие множество А\В⋂С, то все остальные части диаграммы, находящиеся ниже множества В или не относящиеся к пересечению множеств А и С, мы не учитываем.

Таким образом, выделенная область, представляющая множество А\В⋂С, является треугольником, образованным при пересечении пересечения границ множества А и С с границей множества В.

Рисунок, обозначающий выделенную область, представляющую множество А\В⋂С, можно увидеть по ссылке:
https://drive.google.com/file/d/1WEC579srylxUO0ltZCzv0CiCHvYaax4z/view?usp=sharing