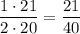Вычислите значение выражения
(1-1/4)*(1-1/9)*(1-1/16) … (1-1/400)
!!
Другие вопросы по теме Математика
Популярные вопросы
- Найдите любые три развязки линейного уравнения с двумя переменными х-у = 10...
3 - К графику заданной функции y=4корень2x+7 проведите касательную так чтобы она...
2 - Представь дроби 1/3 и 1/4 в виде дробей со знаменателем 12:...
2 - Послушайте романс, и ответьте на следующие во Какой характер, настроение этого...
1 - Реши систему:{x=7+y x−2y+2=4х= у=...
3 - Биология. Нужно заполнить эту таблицу...
2 - Придумать краткую, но весёлую рекламу...
1 - Упавши з висоти 20 м,куля масою 5 кг заглиблилась в ґрунт на 10 см. Чому дорівнює...
3 - Какой цвет индикатора фенолфталеина в щёлочной среде ...
2 - Приклади тіл які перебувають у рівновазі?...
2
Пошаговое объяснение:
Каждый множитель имеет вид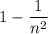 . Преобразуем его:
. Преобразуем его: 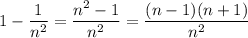 . Распишем произведение в соответствии с преобразованием:
. Распишем произведение в соответствии с преобразованием: 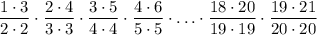
Заметим, что знаменатель n-ного множителя сокращается крайними числами n-1-го и n+1-го числителей. Тогда остаются в знаменателе первого множителя остаётся 2 (не хватает двойки слева для сокращения), в знаменателе последнего — 20 (не хватает двадцатки справа), в числителе первого — 1 (ничего не сокращает слева), в числителе последнего — 21 (ничего не сокращает справа). Получаем выражение