Вычислите предел, используя правило лопиталя (с решением, полностью)

ответ: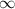

Пошаговое объяснение:

Смотри, тут самое главное - знать таблицу производных.

От 1' = 0

От e^(-x) будет -e^x, но т.к. у тебя еще перед формулой стоит минус, то производная будет просто e^x

От х' = 1

От сos(x)' = -sin(x)

От sin(x)' = cos(x)

Когда нашел первую производную числителя и знаменателя, то подставил снова 0, все равно выходит неопределенность вида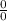 , значит снова находим производную... И так делаем до тех пор, пока не найдем результат.