Вычислите площадь фигуры, ограниченную линиями y=x^2, y=2x

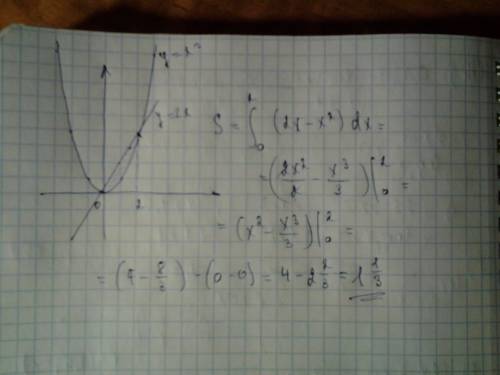
Применены : графики параболы и прямой, формулы интегрирования, формула Ньютона-Лейбница

НАрисуй графики этих функций и ты увидишь, что нижней функцией будет y=x^2, а верхней y=2x, затем найдём точки пересечения приравнял y=x^2 и y=2x, получим x^2=2x, x*(x-2)=0, тоесть данные функции пересекаются в 2 точках, x=0 и x=2, затем вычисляем двойной интеграл , интеграл(от 0 до 2)по dx (интеграл(от 2x до x^2) по dy), поставляя пределы получаем интеграл(от 0 до 2) по dx*(x^2-2x), затем интегрируем и снова подставляем пределы и получаем ((x^3/3)-x^2)в подстановке от 0 до 2, совершаем подстановку и получаем 0^3/3-0^2-(2^3/3-2^2)=-(-4/3)=4/3 ответ: S=4/3