Вычислите площадь фигуры , ограниченной линиями
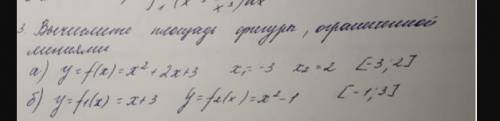
Другие вопросы по теме Математика
Популярные вопросы
- На предприятие поступило растительное масло 600 л. после расфасовки в потребительскую...
1 - Значение слов Второй Восточный Тюркский каганат...
1 - 5 полных и 5 не полных предложений с расказа Моцарт и Сальери ...
3 - ОЧЕНЬ С МОИМ ЗАДАНИЕМ ПО ФИЗИКЕ ТАМ НО ЕСЛИ ПРОДУБЛИРУЕТЕ ОТВЕТ ПОД ЭТОТ...
1 - Решите по действиям очень надо ...
3 - Упражнения 183 русский язык 5класс...
1 - Функция y=4x-9 возрастает или убывает?...
2 - До ть ПОТРІБНО вставити Where who why what how when...
3 - Здравствуйте, нужна по кейсу Маленькая, но достаточно жирненькая мушка...
2 - Нужно выполнить все 5 ex. Делать по образцу. Пустые ответы сразу в бан....
1
ответ: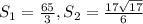
Пошаговое объяснение: