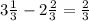Вычислите площадь фигуры ограниченной графиками функций у=х^2+1 и у=-х^2+3
Другие вопросы по теме Математика
Популярные вопросы
- Распределить по классам следующие вещества, указать их названия, общую формулу по...
3 - 1. Какие овощные культуры вы знаете? 2. Какую зелень используют в качестве приправы,...
1 - Вибери правильне твердження 1)усі точки материка Африка мають східну довготу 2)усі...
1 - Write the third person singular of the present simple. Note that sometimes there...
2 - Получите новые глаголы с приставок. ехать,ехать,ехать,ехать,ехать,ехать,ехать,ехать,...
2 - Как вы думаете, почему для России, а затем и СССР было важно поддерживать отношения...
3 - Задание на фото. Задание на фото. ...
2 - 70 ответить на вопросы . 1 Погода - это 2 Какие элементы входят в понятие погода?...
3 - 1. Почему высыхает Аральское море? 2. Как в ОСНОВНОМ образуются горные озера?3....
1 - -22/15×(-4,5)×15/32×(-2/9)...
2
Пошаговое объяснение:
найдем точки пересечения графиков, для этого приравняем правые части уравнений
х^2+1= -х^2+3
2х^2=2
х^2=1, х1=1, х2= -1
Пределы интеграла от -1 до 1
находим определенный интеграл у=х^2+1 в этих пределах
первообразная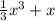 +C
+C
подставляем пределы интегрирования получаем площадь
S1 = 1/3 + 1 -(-1/3 -1)=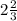
находим определенный интеграл у=-х^2+3
первообразная -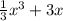 +C
+C
подставляем пределы интегрирования получаем площадь
S2 = -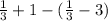 = 4 -
= 4 - 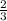 =
=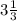
S=