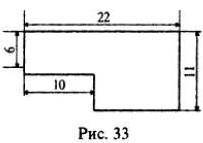
Вычислите периметр и площадь фигуры изображённый на рисунке 33 (измерения даны в сантиметрах) ​

периметр=66 см

площадь=192 см²

Пошаговое объяснение:

периметр=короче это такая задача со ступеньками этот угол можно переместить и получить прямоугольник.

2464646464646/3161534

Хорошо, давайте рассмотрим данную фигуру и подсчитаем ее периметр и площадь.

На рисунке 33 изображена фигура, состоящая из двух треугольников и двух прямоугольников. Для начала определим измерения сторон каждой фигуры:

1) Наибольший треугольник:
Трапеция ABDC, где стороны AB и CD - основания, а сторона AD - высота.
Исходя из рисунка, видно, что основания AB и CD равны 8 см и 12 см соответственно.
Высота AD не указана на рисунке, поэтому мы не можем ее определить точно, но для расчетов можем считать высоту AD равной 7 см (это приближенное значение, оцененное по рисунку).

2) Маленький треугольник:
Нарисован справа от большого треугольника и является прямоугольным.
Гипотенуза FG = 5 см, отрезки EJ и GJ - катеты.
Катет EJ указан на рисунке и равен 3 см.
Катет GJ можно вычислить, применив теорему Пифагора:
GJ^2 = FG^2 - EJ^2 = 5^2 - 3^2 = 25 - 9 = 16.
Получаем, что GJ = √16 = 4 см.

3) Прямоугольники:
Прямоугольники ABCG и CDEF расположены между треугольниками.
На рисунке указаны основания BC и EF, которые равны 8 см и 4 см соответственно.
Высота прямоугольников AB и CD не указана на рисунке, для расчетов возьмем высоты AB и CD равными по 7 см (это приближенные значения, оцененные по рисунку).

Теперь, когда у нас есть измерения, можем перейти непосредственно к вычислениям:

1) Периметр:
Периметр - это сумма длин всех сторон фигуры.
Для вычисления периметра сложим длины всех сторон:
Периметр = AB + BC + CG + GF + FE + ED + DA
= 8 + 8 + 7 + 5 + 4 + 4 + 12
= 48 см.

2) Площадь:
Площадь - это количество пространства, закрытого фигурой.
Для вычисления площади разделим фигуру на несколько простых фигур (треугольники и прямоугольники), вычислим площади каждой из них и затем сложим результаты.

• Площадь большего треугольника:
Площадь треугольника можно вычислить по формуле:
Площадь = (основание * высота) / 2.
Подставим значения оснований AB = 8 см и CD = 12 см, и высоты AD = 7 см:
Площадь большего треугольника = (8 * 7) / 2 = 56 / 2 = 28 см².

• Площадь маленького треугольника:
Маленький треугольник - это прямоугольный треугольник.
Площадь прямоугольного треугольника можно вычислить по формуле:
Площадь = (катет * катет) / 2.
Подставим значения катетов EJ = 3 см и GJ = 4 см:
Площадь маленького треугольника = (3 * 4) / 2 = 12 / 2 = 6 см².

• Площадь прямоугольников:
Площадь прямоугольника вычисляется как произведение длины на ширину.
Подставим значения длины и ширины каждого прямоугольника:
Площадь первого прямоугольника ABCG = 8 * 7 = 56 см².
Площадь второго прямоугольника CDEF = 4 * 7 = 28 см².

Теперь сложим площади всех фигур:
Площадь фигуры = Площадь большего треугольника + Площадь маленького треугольника + Площадь первого прямоугольника + Площадь второго прямоугольника
= 28 + 6 + 56 + 28
= 118 см².

Таким образом, периметр фигуры равен 48 см, а площадь фигуры равна 118 см².