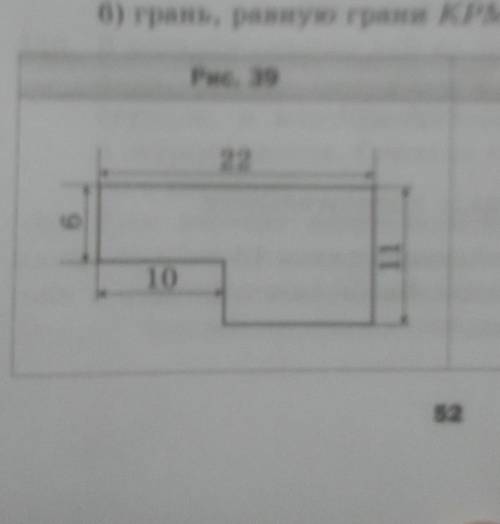
Вычислите периметр и площадь фигуры, изображённой на рисунке 39 ( размеры даны в сантиметрах ).

периметр это когда всё стороны складываешь тоесть 22+11+10+6=49см площадь это когда длину на ширину умножаем 11•22

Хорошо, давайте вычислим периметр и площадь фигуры на рисунке 39.

Периметр фигуры - это сумма длин всех сторон. Для этого нам нужно измерить каждую сторону и сложить их значения.

На рисунке 39 видно, что фигура имеет форму прямоугольника с прикрепленным треугольником. Давайте вычислим периметр прямоугольника.

Периметр прямоугольника вычисляется по формуле P = 2*(a + b), где a и b - длины двух сторон прямоугольника.

Длина одной стороны прямоугольника равна 15 см, а длина второй стороны равна 10 см. Подставим значения в формулу:

P = 2*(15 + 10) = 2*(25) = 50 см.

Таким образом, периметр прямоугольника равен 50 см.

Теперь вычислим периметр треугольника. У треугольника три стороны, поэтому периметр можно найти, сложив длины всех трёх сторон.

Стрелка указывает нам, что сторона треугольника имеет длину 10 см.

P = 10 + 10 + 15 = 35 см.

Теперь, чтобы получить полный периметр фигуры, нужно сложить периметр прямоугольника и периметр треугольника:

50 см (периметр прямоугольника) + 35 см (периметр треугольника) = 85 см.

Таким образом, периметр всей фигуры на рисунке 39 равен 85 см.

Теперь перейдем к вычислению площади фигуры.

Площадь прямоугольника вычисляется по формуле S = a * b, где a и b - длины сторон прямоугольника.

Длина одной стороны прямоугольника равна 15 см, а другой стороны - 10 см. Подставим значения в формулу:

S = 15 * 10 = 150 квадратных сантиметров.

Теперь посчитаем площадь треугольника.

Площадь треугольника можно найти, используя формулу S = (a * h)/2, где a - основание треугольника, а h - высота треугольника. На рисунке видно, что основание треугольника равно 15 см, а высоту треугольника нужно найти.

Чтобы найти высоту треугольника, проведем от основания до вершины перпендикулярную линию. Так как треугольник равнобедренный, высота будет делить основание пополам.

Таким образом, высота треугольника равна 10 см.

Теперь подставим значения в формулу:

S = (15 * 10)/2 = 150/2 = 75 квадратных сантиметров.

Таким образом, площадь треугольника равна 75 квадратных сантиметров.

Чтобы найти полную площадь фигуры, нужно сложить площади прямоугольника и треугольника:

150 квадратных сантиметров (площадь прямоугольника) + 75 квадратных сантиметров (площадь треугольника) = 225 квадратных сантиметров.

Таким образом, площадь всей фигуры на рисунке 39 равна 225 квадратных сантиметров.