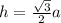Вычислите объем правильной треугольной пирамиды, сторона основания которой 6 см, высота 9 см
Другие вопросы по теме Математика
Популярные вопросы
- Если температура воздуха на верху холма 11 с, то какая температура...
2 - Найдите приращение к функции y=f(x) при переходе от точки х к точке...
1 - 1. как измениться концентрация 15% раствора массой 150 г., если...
3 - Написать сочинение кем быть (если что я хочу быть ветеринаром)...
1 - Маркетинг – это: а) процесс планирования и воплощения замысла,...
2 - Назовите номера предложений, синонимичных данным: 1. die maschinenbauer...
1 - Всемирная сделайте сравнительную таблицу развития национального...
2 - Ex. 3. a) supply the correct prepositions where necessary. andreev...
3 - Употребите нужную степень сравнения прилагательных, данных в скобках:...
1 - Решите уравнение x^2-5/x-1 = 3x+2/x...
1
Дано: SABC- правильная пирамида, SO- высота, SO=9 см, AB=Bc=AC=6 см.
ответ: 27√3 см³
Использовались формулы:
1) Объем пирамиды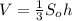
2) Площадь треугольника: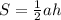
3) высота равностороннего треугольника: