Вычислите неопределённый интеграл, 3 примера Не через photomath
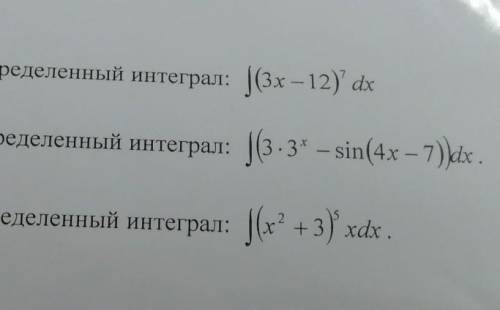
Другие вопросы по теме Математика
Популярные вопросы
- Площадь прямоугольника равна 15/16м2.Найдете прериметр прямоугольника, если...
3 - 2. Конструкция To be going to do something. Заполните пропуски, употребив правильную...
1 - 2) Начертите на координатной плоскости: 1) ломаную с вершинами в точках (0;...
2 - Що таке система розселення? Назвіть типи поселинь? Які функції вони виконують!...
1 - Если в течении суток самая высокая температура +4°С, а самая низкая -10°С,...
3 - Вычислите площадь фигуры ограниченной линиями: y= -0.5x^2+2x y=-0.5x+2...
2 - Доповнити речення частками:Дозвольте ... мені ...слова все ... мовити...
1 - 18. НЕ відокремлюється прикладка в реченні (роA I Андрюша цей невеселий комунар...
2 - В основании треугольной призмы прямоугольный треугольник с катетами 6см и 8см....
3 - 4) Синтаксическийразбор предложения.Моё вниманиепривлёк зелёныйкузнечик, он...
3
ответ: 1) 1/24*(3*x-12)⁸+C; 2) 3*3ˣ/ln3+1/4*cos(4*x-7)+C, 3) 1/12*(x²+3)⁶+C.
Пошаговое объяснение:
1) ∫(3*x-12)⁷*dx=1/3*∫(3*x-12)⁷*d(3*x-12)=1/24*(3*x-12)⁸+C.
2) ∫[3*3ˣ-sin(4*x-7)]*dx=3*∫3ˣ*dx-1/4*∫sin(4*x-7)*d(4*x-7)=3*3ˣ/ln3+1/4*cos(4*x-7)+C.
3) ∫(x²+3)⁵*x*dx=1/2*∫(x²+3)⁵*d(x²+3)=1/12*(x²+3)⁶+C.