Вычислите не собственный интеграл или доказать его расходимость
Другие вопросы по теме Математика
Популярные вопросы
- Задание по математике номер 2.1 A(1-5)...
1 - Поведенье и поступки каир хана...
1 - Сделайте PEST-анализ по развитию органического сельского хозяйства в РК...
2 - Мы поняли , что 1 china,3 brazil,4 canada, 5 germany,6 egypt . можете подсказать...
3 - Дополните предложения,используя слова,данные в скобках.1. ... всегда поддерживались...
2 - мне это сор по алгебре 7 класс...
1 - Когда прекратили подписывать деньги в россии? 1930 1950 1970 1990...
1 - Present perfect simple Put the verb into the correct form, (present perfect...
1 - До ть з алгеброюЗбірник контрольних та самостійних робіт варіант 2 Номер...
3 - Grammar D. Complete the table....
1
Поскольку несобственный интеграл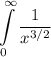 сходится, то сходиться будет интеграл
сходится, то сходиться будет интеграл 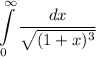 (первый признак сравнения).
(первый признак сравнения).