Вычислите количество необходимых для рассадки 4-х гостей на 8-ми стульях

Ответы

SuperDusia 16.07.2020 20:56

Пошаговое объяснение:

1) Сначала определим количество выборов стульев для гостей.

Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).

Число сочетаний из n элементов по k обозначается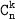 $\tt \displaystyle C^{k}_{n}$ и равно:

$\tt \displaystyle C^{k}_{n} = \frac{n!}{k! \cdot (n-k)!} ,$

где m!=1·2·3·...·(m-1)·m.

Тогда, по условию задачи общее количество стульев n=8 и нужно выбрать стульев k=4:

$\tt \displaystyle C^{4}_{8} = \frac{8!}{4! \cdot (8-4)!} = \frac{8!}{4! \cdot 4!}.$

2) Теперь определим количество рассадки 4-х гостей на 4-х стульях. Так как каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:

P₄=4!.

3) Количество необходимых для рассадки 4-х гостей на 8-ми стульях определим как произведения число сочетаний на перестановку:

$\tt \displaystyle C^{4}_{8} \cdot P_{4} = \frac{8!}{4! \cdot 4!} \cdot 4!=\frac{8!\cdot 4!}{4! \cdot 4!} =\frac{8!}{4!} =\frac{4! \cdot 5 \cdot 6\cdot 7 \cdot 8}{4!} =5 \cdot 6\cdot 7 \cdot 8=1680.$