1. Математика
  2. Вычислите cosa, если tga=-3/4,

Вычислите cosa, если tga=-3/4, п/2 только подробно объясните .

mruzer1999 mruzer1999    2   26.10.2019 16:15    0

Ответы
анаркааа54 анаркааа54  10.10.2020 09:46

Пошаговое объяснение:

Вспоминаем основное тригонометрическое тождество:

sin^2a+cos^2a=1

И то, что такое tga:

tga=\frac{sina}{cosa}

Разделим основное тригонометрическое тождество на cos^2a:

sin^2a+cos^2a=1 \ |\ cos^2a\\tg^2a+1=\frac{1}{cos^2a}

Выразим отсюда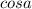 cosa:

tg^2a+1=\frac{1}{cos^2a}\\cos^2a=\frac{1}{tg^2a+1}\\cosa=\sqrt{\frac{1}{tg^2a+1}}=\frac{1}{\sqrt{tg^2a+1}}}

Подставим:

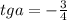1) tga=-\frac{3}{4}:

cosa=\frac{1}{\sqrt{tg^2a+1}}}=\frac{1}{\sqrt{(-\frac{3}{4})^2+1}}}=\frac{1}{\sqrt{\frac{9}{16}+1}}}=\frac{1}{\sqrt{\frac{25}{16}}}}=\sqrt{\frac{16}{25}}=\frac{4}{5}

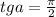2) tga=\frac{\pi}{2}:

cosa=\frac{1}{\sqrt{tg^2a+1}}}=\frac{1}{\sqrt{(\frac{\pi}{2})^2+1}}}=\frac{1}{\sqrt{\frac{\pi^2}{4}+1}}}=\frac{1}{\sqrt{\frac{\pi^2+4}{4}}}}=\frac{\sqrt{4}}{\sqrt{\pi^2+4}}=\frac{2}{\sqrt{\pi^2+4}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Artemko1337 Artemko1337  22.01.2022 05:59
Опять непонятно.. 54/62-x/62=21/62 Надо х (Дроби)...
Данилкамастре Данилкамастре  22.01.2022 05:55
Дано, что sin x = 0.6 и 0 x п/2 . вычисли а) sin 2x б) ctg 2x...
Mellisa11111111 Mellisa11111111  22.01.2022 05:55
Чтобы накачать в бак 120 литров воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 82,5 литра воды. За одну минуту можно выкачать на 4,5 литра...
algriskova06 algriskova06  22.01.2022 05:54
, решать обязательно с пропорции....
Лизочка2597 Лизочка2597  22.01.2022 05:52
Длинна прямоугольника равна в три раза больше его ширины .Если Периметр бассейна составляет 216м , найди ширину бассейна...
m3rry1 m3rry1  22.01.2022 05:52
Одна конфета стоит 60 коп. сколько будет стоить 1000 конфетРешение...
эд104267 эд104267  22.01.2022 05:51
Постройте равнобедренный треугольник с периметром 10 см, боковая сторона которого составляет 30% от периметра. Укажите длины сторон треугольника....
tori201512 tori201512  22.01.2022 05:49
905. (Усно) Яким числом є число -р, якщо: 1) p — додатне число; 2) p = 0; 3) р — від ємне число?...
qwetdfgdsa qwetdfgdsa  22.01.2022 05:47
-5(z-7)+14=30-(2z+1)+12как решить??...
lerka22222222222222 lerka22222222222222  22.01.2022 05:46
Первообразная для функции x квадрате плюс х...

Популярные вопросы