1. Математика
  2. Вычислите: a) lim x^2+3/ x+1=

Вычислите: a) lim x^2+3/ x+1=
x➡1
b) lim x^2+3x+2 / x+1 =
x➡-1

Alesha2112 Alesha2112    1   25.01.2021 16:41    0

Ответы
aselznala2004 aselznala2004  24.02.2021 16:53

Пошаговое объяснение:

а)

\displaystyle \lim_{x \to 1} \frac{x^2+3}{x+1} = \lim_{x \to 1} \frac{1^2+3}{1+1} = 2

b)

\displaystyle \lim_{x \to {-1}} \frac{x^2+3}{x+1}

здесь двустороннего предела не существует.

ищем предел слева и справа

предел слева

\displaystyle \lim_{x \to {-1^-}} \frac{x^2+3}{x+1}= \lim_{x \to {-1^-}} \frac{1}{x+1}* \lim_{x \to {-1^-}} (x^2+3)=\lim_{x \to {-1^-}} \frac{1}{x+1}*4

поскольку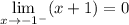  \displaystyle \lim_{x \to {-1^-}}(x+1) = 0  и (х +1) < 0 для всех х < -1, то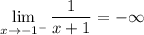 \displaystyle \lim_{x \to {-1^-}} \frac{1}{x+1} = - \infty

итак, предел слева

\displaystyle \lim_{x \to {-1^-}} \frac{x^2+3}{x+1}= 4*-\infty=- \infty

предел справа ищем аналогично, только поскольку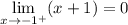 \displaystyle \lim_{x \to {-1^+}}(x+1) = 0

и (х +1) > 0 для всех х > -1, то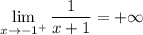      \displaystyle \lim_{x \to {-1^+}} \frac{1}{x+1} = + \infty

и предел справа

\displaystyle \lim_{x \to {-1^+}} \frac{x^2+3}{x+1}= + \infty

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Миксеры Миксеры  16.07.2019 06:10
Решить уравнения 40-х=25 х+28=71 х-31=49 34+х=62 х+29=74 100-х=37...
SanyaZv SanyaZv  16.07.2019 06:10
Собака погналась за кошкой которая находит находилась от неё на расстоянии 270 метров кошка убегает от собаки со скоростью 320 метров в минуту собака бежит со скоростью 350...
lazmax2000 lazmax2000  16.07.2019 06:10
Определи возраст старика хоттабыча если известно чт он больше самого трехзначного числа на двузначное число сумма цивр этого двузночного числа делится на 3 а их разность равна...
vladykasevera vladykasevera  16.07.2019 06:10
Впарке посадили 4 рядатюльпанов по 9 в каждом ряду и столько же по 6 рядов нарцисов .сколько тюльпан и нарцисов посадили в парке.надо решить двумя...
arinka90 arinka90  16.07.2019 06:10
Сколько: граммов в 1/2 кг, 3/4 кг, 7/20 кг минут в 1/2 ч, 3/4 ч, 5/6 ч квадратных метров в 1/2 га, 1/4 га, 3/4 га кубических сантиметров в 1/2 м(в кубе) 1/5 м(в кубе) 2/5 м(в...
2345Pomogite2345 2345Pomogite2345  16.07.2019 06:10
Один рабочий красит забор за 4 часа . сколько заборов покрасят трое рабочих за 8 часов...
normanajas15 normanajas15  16.07.2019 06:10
Банки 3 литр березового сока а в другой 2 литра меньше сколько литров сока во второй банке...
tarassedelniko tarassedelniko  16.07.2019 06:10
Шестеро друзей соревновались в дартс. на вопрос, какое каждый из них занял место, андрей сказал: я был вторым, боря- третьим . евгений возразил: нет, боря был вторым, андрей-...
slavasolyanin slavasolyanin  16.07.2019 06:10
Из двух городов расстояние между которыми 520 км одновременно вышли навстречу друг другу два поезда и встретились через 4 часа один поезд шел со средней скоростью 60км/ч с какой...
milenasalikova milenasalikova  16.07.2019 06:10
Решите .я решил, но не уверен с ответом.y=(3x+2)*(x^2+4x-1) решить производную ф-цию...

Популярные вопросы