Вычислить y'(0) если y=x2-x

-1

Пошаговое объяснение:

y=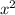-x

y`=2x-1

y`(0)=2*0-1

y`(0) = -1

Для того чтобы вычислить y'(0) (производную функции y по переменной x в точке x=0), нам понадобится применить правило дифференцирования для каждого слагаемого функции y=x^2 - x.

Для первого слагаемого x^2, его производная будет вычислена по правилу степенной функции, где степень умножается на коэффициент перед переменной и затем степень уменьшается на единицу. Давайте вычислим это:
d/dx (x^2) = 2x

Для второго слагаемого -x, его производная будет равна -1, так как производная константы равна нулю.

Теперь нам нужно сложить найденные производные каждого слагаемого, чтобы получить производную функции y. То есть, y'(x) = 2x - 1.

Чтобы вычислить y'(0), мы подставляем значение x=0 в полученную производную функцию. Давайте это сделаем:
y'(0) = 2 * 0 - 1 = -1

Итак, получается, производная функции y=x^2 - x в точке x=0 равна -1.