Вычислить tg(α-30°),если cosα=1/√2 и 0<α<π/2
Другие вопросы по теме Математика
Популярные вопросы
- Примеры 2-ух чисел с разными знаками, сумма которых равна: 1)10...
1 - 1) найдите расстояние между точками x(1,0) и y(5,0). 2)решите...
3 - Выписано несколько последовательных членов арифметической прогрессии:...
1 - Вкниге 35 сказок. к каждой сказке художник сделал по 2 иллюстрации....
2 - Выпишите словосочетания сущ+прил и поставте их в т.п., п.п 1....
1 - Задан равнобедренный треугольник, периметр которого 18см.рассчитайте...
3 - Что вы знаете о первом поселении первых поселенцах и колонистах?...
1 - Белочки нашли несколько орехов и стали их делить.если каждая белочка...
1 - Що означає образ чайки для українського народу...
1 - Есть 37 литров бензина,сколько км.проеду при расходе 8 литров...
1
Но т.к.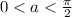 , то
, то 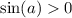 поэтому
поэтому