1. Математика
  2. Вычислить производные сложных

Вычислить производные сложных функций: задания на фото(на слова правило,формула и т.д в скобках-не обращайте внимание)


Вычислить производные сложных функций: задания на фото(на слова правило,формула и т.д в скобках-не о

katenok1706 katenok1706    3   25.11.2020 14:11    4

Ответы
главный13 главный13  25.12.2020 14:14

До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)

Пошаговое объяснение:

1) Производная произведения: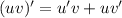 (uv)'=u'v+uv'

u = 5^{x+3} \\v = cos(7x)

Правило дифференцирования сложной функции:(f(g(x)))'_{x} = (f(g(x)))'_{g}*(g(x))'_{x}   (индекс внизу означает, по какой переменной дифференцируем, * означает умножение)

u' = 5^{x+3} ln(5) (x+3)' = 5^{x+3} ln(5) \\v' = -sin(7x) (7x)' = -7sin(7x)

тогда (5^{x+3}cos(7x))' = cos(7x)5^{x+3} ln(5)-7sin(7x)5^{x+3} = 5^{x+3}(cos(7x) ln(5)-7sin(7x))

2) Дифференцирование сложной функции (f(g(x)))'_{x} = (f(g(x)))'_{g}*(g(x))'_{x}

Примем f(g) = e^{g}, g(x) = cos(x^2)

Дифференцируем f(g):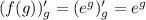  (f(g))'_{g} = (e^{g})'_{g} = e^{g}

Дифференцируем g(x): (g(x))'_{x} = (cos(x^2))'_{x} = (cos(x^2))'_{x^2}(x^2)'_{x} = -sin(x^2)2x

Тогда

(f(g(x)))'_{x} = e^{cos(x^2)}*(-2xsin(x^2))

3) Как и в 2, дифференцируем сложную функцию

(\sqrt{1+ln^2(x)} )'_x = (\sqrt{1+ln^2(x)} )'_{ln^2(x)}*(ln^2(x))'_{ln(x)}*(ln(x))'_x=\\=\frac{1}{2\sqrt{1+ln^2(x)} } 2ln(x)\frac{1}{x} = \frac{ln(x)}{x\sqrt{1+ln^2(x)} }

4) Производная суммы есть сумма производных:

(f(x)+g(x))' = f'(x)+g'(x)

f(x) = x, g(x) = -2arcctg(3x^2)\\f'(x) = 1\\g'(x) = (-2arcctg(3x^2))' =-2 (arcctg(3x^2))' = -2 (arcctg(3x^2))'_{3x^2}*(3x^2)'_x=-2(-\frac{1}{1+(3x^2)^2} )*3*2x =\frac{12x}{1+9x^4}

Окончательно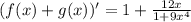 (f(x)+g(x))' = 1+\frac{12x}{1+9x^4}

5) Опять производная сложной функции:

(tg^3(x+1))'_x = (tg^3(x+1))'_{tg(x+1)}*(tg(x+1))'_{(x+1)}*(x+1)'_x= 3tg^2(x+1)*\frac{1}{cos^2(x+1)} *1 = \frac{3tg^2(x+1)}{cos^2(x+1)}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
elinochka0707 elinochka0707  29.09.2019 01:10
Теперь вы в продуктовом магазине покупаете овощи и фрукты пакет выдерживает груз до 5 кг можете ли вы положить в него и 950 г помидоров 1 кг 30 граммов огурцов 1 кг 700 г яблок или...
denisDergunov denisDergunov  29.09.2019 01:10
С! некто работает 24 дня в месяц,тратит в каждый из тридцати дней по 50руб и откладывает за месяц 900 руб.сколько он получает за рабочий день?...
Alexandra335 Alexandra335  29.09.2019 01:10
По записи числа выберите суммы значения которых делятся на 22 на 5...
Raffee Raffee  29.09.2019 01:10
Водном кошельке на 35 рублей больше, чем в другом, причем 1/3 денег, имеющихся в первом кошельке, равна 3/4 денег, имеющихся во втором кошельке. сколько денег во втором кошельке...
GromKR GromKR  29.09.2019 01:10
Сколько существует двехзначных чисел у которых вторая цифра больще первой?...
Даниэла2106 Даниэла2106  29.09.2019 01:10
Баба света решила сварить варенье. у нее получилось 8 кг, при этом ягоды составили 70%. ее внучка маша попробовала и ей оно показалась кислым, поэтому втайне от бабушки она добавила...
Артём00071 Артём00071  29.09.2019 01:10
3×(-27)в степени 1/3 - 0,1×81 в степени 3/+1...
maritsumie maritsumie  29.09.2019 01:10
За два дня велосипед проехал 272 км, причем в первый день он проехал 13/17 всего пути. сколько километров он проехал во второй день?...
onexochu onexochu  29.09.2019 01:10
5класс на каждом этаже жилого дома по три квартиры может ли быть что всего в подъезде 27 32 квартиры 69 квартир...
dilnaz7771 dilnaz7771  29.09.2019 01:10
Длина классной комнаты 12м,а ширина составляет одну вторую её часть.чему равна ширина классной комнаты. вычисли объем воздуха в классной комнате...

Популярные вопросы