1. Математика
  2. Вычислить производную второго

Вычислить производную второго порядка

Wertwer123 Wertwer123    1   13.02.2020 02:24    4

Ответы
fukkacumi2017 fukkacumi2017  11.10.2020 04:16

y = \dfrac{x^{2} - 1}{x^{2} + 1}

Найдем первую производную (производную первого порядка):

y' = \left(\dfrac{x^{2} - 1}{x^{2} + 1} \right)' = \dfrac{(x^{2} - 1)'(x^{2} + 1) - (x^{2} + 1)' (x^{2} - 1)}{(x^{2} + 1)^{2}} =\\= \dfrac{2x(x^{2} + 1) - 2x(x^{2} - 1)}{(x^{2} + 1)^{2}} = \dfrac{2x(x^{2} + 1 - x^{2} + 1)}{(x^{2} + 1)^{2}} = \dfrac{4x}{(x^{2} + 1)^{2}}

Производная второго порядка (вторая производная) есть первая производная от производной первого порядка, то есть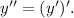 y'' = (y')'.

Найдем вторую производную (производную второго порядка):

y'' = \left(\dfrac{4x}{(x^{2} + 1)^{2}} \right)' = \dfrac{(4x)'(x^{2} + 1)^{2} - ((x^{2} + 1)^{2})'4x}{(x^{2} + 1)^{4}} =\\= \dfrac{4(x^{2} + 1)^{2} - 16x^{2}(x^{2} + 1)}{(x^{2} + 1)^{4}} = \dfrac{4(x^{2}+1)(1 - 3x^{2})}{(x^{2} + 1)^{4}} = \dfrac{4 - 12x^{2}}{(x^{2} + 1)^{3}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
MELL111111 MELL111111  05.06.2019 10:00
Сумма 2 рациональных чисел равна 2490. найдите эти числа, если 6,5% одного из них равны 8,5 % другого...
sladkaezhka19 sladkaezhka19  05.06.2019 10:00
Расположите цифры в порядке убывания: расположите цифры в порядке убывания: 195840 , 348384 , 1293568 , 37779 ,659175 , 813568?...
026k 026k  05.06.2019 10:00
Решить . цена за 1 метр ткани 510 тенге. какова стоимость 2,63 метров ткани? округлите до десятков....
dashok270307 dashok270307  05.06.2019 10:00
Периметр прямоугольника равен тридцати шести сантиметров найдите его площадь если ширина прямоугольника равна шести сантиметров...
manawer manawer  05.06.2019 10:00
Длина отрезка 168 см. этот отрезок разделен на 3 отрезка .второй отрезок в 3 раза длиннее чем первый а третий в 4 раза длиннее чем первый найди длину каждого отрезка...
Алёна345135537 Алёна345135537  05.06.2019 10:00
Простыня, норма расхода 2м,количество изделий 8 пр.пододеяльник норма расхода 4м.количество изделий 6 п.всего использовано ? м....
Shvets73 Shvets73  05.06.2019 10:00
Пальто продавалась по цене 1500 руб сколько рублей стало стоить пальто после снижения его цены на 20%...
smaliar2004 smaliar2004  05.06.2019 10:00
Сколько будет 2+2=? незнаю сколько будет...
kayumovtanvir89 kayumovtanvir89  05.06.2019 10:00
Два самолёта летели с одинаковой скоростью ,один самолет был в воздухе 3 часа другой 5 часов и пролетел на 1600 км больше,чем первый.поставь вопрос и реши...
jybais228 jybais228  05.06.2019 10:00
Из пункта а в пункт в одновременно выехали два автомобиля.первый проехал с постоянной скоростью весь путь.второй проехал первую половину пути со скоростью 44км/ч ,а вторую половину...

Популярные вопросы