Вычислить предел с правила Лопиталя: 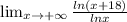
Другие вопросы по теме Математика
Популярные вопросы
- Яка кількість теплоти необхідна щоб розплавити 50 грам золота взятого...
2 - Каким давлением 4 грамма кислорода, заключённые в одном кубическом метре...
3 - От чего зависит авторитет руководителя? ...
2 - До поданих слів доберіть омоніми. вкажіть вид омонімів.1 мул, поза,гірка,настав...
3 - Основной торговой партнер древней руси а) византия б) швеция в тмутаракань...
1 - Вычислить работу силы f = {3; -2; 4}, если ее точка приложения двигалась...
1 - Решите а1 весь, с полным описанием примеров, 30 !...
3 - 30 ! сопостовительная характеристика остапа и андрия 1) первое впечатление...
1 - Первоначальная длина пружины 12 см, после того как был подъвешин груз...
3 - По рисункам определите методы иследований...
2
Применяем правило Лопиталя.
1
Пошаговое объяснение:
x'=1
18'=0
т.к. производная числителя и знаменателя при х стремящемся к бесконечности существует, то можно применять правило Лопиталя.
производная числителя равна (1/(х+18))*(х+18)'=1/(x+18)
производная знаменателя равна 1/х;
предел отношения (1/(х+18)):(1/х)=х/(х+18) равен коэффициенту при х, т.е 1, т.к. числитель и знаменатель - многочлены первой степени, а х стремится к +∞