Вычислить предел функции
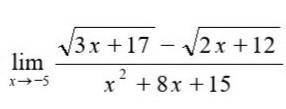
Другие вопросы по теме Математика
Популярные вопросы
- 4. Изучите теоретический материал. Запишите 3-4 предложения с местоиме ниями...
3 - Қазақ тілі 7 сынып бжб помагите...
3 - Запишите числа в порядке возрастания: 6,415; 6,02; 6,91; 6,007; 6,13. ...
3 - Необычайное Приключение бывшее с Владимиром маяковским вопросы...
2 - К чему близок рассказ как я стал писателем ? : К воспоминаниямДневниковым записямИли...
3 - Die Wiederholung der Präpositionen (mit dem Dativ)1. Elena schreibt……..dem Kugelschreiber....
1 - История появления праздника Корнями история празднования Нового Года уходит в...
3 - Центральная симметрия. Осевая симметрия. Урок 3 дан равнобедренный треугольник...
1 - ответить на вопрос по структуре ПОПС《с чем связано торговое соперничество государств...
1 - Task 3. Choose the correct item. “Will it snow today?” “No, it … “.a. ...
1
Пошаговое объяснение: