1. Математика
  2. Вычислить площадь треугольника

Вычислить площадь треугольника , вершинами которого служат точки а (4,2), в (9,4), с (7,6) (написать решение)

Никита0234632 Никита0234632    1   18.03.2019 03:30    0

Ответы
niktikhonov19 niktikhonov19  25.05.2020 22:20

по формуле расстояния между двумя точками, заданными координатами

d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}

 

AB=\sqrt{(4-9)^2+(2-4)^2}=\sqrt{29};\\ BC=\sqrt{(9-7)^2+(4-6)^2}=2\sqrt{2};\\ AC=\sqrt{(4-7)^2+(2-6)^2}=5

Полупериметр равен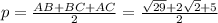 p=\frac{AB+BC+AC}{2}=\frac{ \sqrt{29}+2\sqrt{2}+5}{2}

 

По формуле Герона площадь равна

S=\sqrt{p(p-a)(p-b)(p-c)}=\\ \sqrt{\frac{\sqrt{29}+2\sqrt{2}+5}{2}*(\frac{\sqrt{29}+2\sqrt{2}+5}{2}-5) *(\frac{\sqrt{29}+2\sqrt{2}+5}{2}-2\sqrt{2})*(\frac{\sqrt{29}+2\sqrt{2}+5}{2}-\sqrt{29})}=\\ \sqrt{\frac{\sqrt{29}+2\sqrt{2}+5}{2}*(\frac{\sqrt{29}+2\sqrt{2}-5}{2}) *(\frac{\sqrt{29}-2\sqrt{2}+5}{2})*(\frac{-\sqrt{29}+2\sqrt{2}+5}{2})}=\\ \frac{1}{4}\sqrt{ (\sqrt{29}+2\sqrt{2})+5)*((\sqrt{29}+2\sqrt{2})-5) *(5+(\sqrt{29}-2\sqrt{2}))*(5-(\sqrt{29}-2\sqrt{2}))}=

\frac{1}{4}\sqrt{ (\sqrt{29}+2\sqrt{2})^2-5^2)*(5^2-(\sqrt{29}-2\sqrt{2})^2)}=\\ \frac{1}{4}\sqrt{ (29+8+4\sqrt{58}-25)*(25-29-8+4\sqrt{58})}=\\ \frac{1}{4}\sqrt{ (12+4\sqrt{58})*(-12+4\sqrt{58})}=\\ \frac{4}{4}\sqrt{ (\sqrt{58}+3)*(\sqrt{58}-3)}=\\ \sqrt{ (\sqrt{58})^2-3^2)}=\\ \sqrt{58-9}=\sqrt{49}=7

 ответ: 7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Лизок070707 Лизок070707  01.03.2019 23:30
Решите уравнение х+56=95, у-67=41, 86-z=39,(68-m)+16=24, 85-(14+n)=68...
DanilBeast DanilBeast  01.03.2019 23:30
Вычислите значение выражения: 1. 2,63х+12,3у если х=0,23 а у=0,84 2. х(во второй степени)-1.3х если х=11.3...
matuxh matuxh  01.03.2019 23:30
Разложите множтели на многочлен 1.3(2х+5)+х(5+2х) 2.5а(х-у)+3(х-у)...
1inks 1inks  01.03.2019 23:30
Уменьшите: 4ч 48мин в 4 раза,2ч 55мин в 5 раз...
mamaamamma33 mamaamamma33  01.03.2019 23:30
Выражения, ну как легче короче. (6а+7в)*14 10*(14x - 27у + 5) 4*(31с - 17 + 54d)...
bogussasa7 bogussasa7  01.03.2019 23:30
Увеличте: 1ч 20мин в 4 раза,2ч 12мин в 7 раз...
НиколайСПБ НиколайСПБ  01.03.2019 23:30
Аквариум имеет форму прямоугольного параллелепипеда. его боковые стенки стеклянные.определите площадь поверхности стекла, если длинна аквариума 50 см, ширина 25 см, а высота...
AnastasiaKT AnastasiaKT  01.03.2019 23:30
Разделите числитель на знаменатель и выразите обыкновенную дробь в виде десятичной,округлив с точностью до 0,01. 3/6= 6/15= 19/23= 2целых/5/20= 4/31=...
nick121201 nick121201  01.03.2019 23:30
Соревнование по биатлону состоят из лыжной гонки и стрельбыпо мешеням трассу длиной 7 с половиной километров спортсмен за 25 минут с какой скоростью шёл спортсмен если стрельба...
СашаСтрела СашаСтрела  01.03.2019 23:30
Пусть одна тетрадная клетка изображает участок площадью 50 кв.м.изобразите прямоугольный участок площадью 6а...

Популярные вопросы