1. Математика
  2. Вычислить площадь криволинейной

Вычислить площадь криволинейной трапеции, ограниченной линиями: f(x)=1-x^2, x=-1; y=0 f(x)=-x^2-2x+2, y=0; x=-1; x=0

Flashvinchester Flashvinchester    1   02.10.2019 05:30    0

Ответы
bobrikov01 bobrikov01  09.10.2020 11:04

а) Найдем точки пересечения функции 1 - x^2 с осью OX

1 - x^2 = 0

x1 = -1

x2 = 1

Следовательно для нахождения площади криволинейной трапеции нам надо найти

\int\limits^1 _ {-1} {(1-x^{2})} \, dx

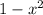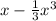
Первообразная функции 1-x^{2} равна x-\frac{1}{3} x^{3}

Следовательно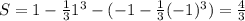 S=1-\frac{1}{3} 1^{3}-(-1-\frac{1}{3} (-1)^{3})=\frac{4}{3}

б) Здесь пределы интегрирования определены, поэтому находим

\int\limits^{0}_{-1} {(x^{2}-2x+2)} \, dx

Первообразная в этом случае:

F(x)=\frac{1}{3} x^{3}-x^{2}+2x

S=F(0)-F(-1)=-(\frac{1}{3} (-1)^{3}-(-1)^{2}+2*(-1))=\frac{1}{3}+1+2=3\frac{1}{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
рябиночка17 рябиночка17  17.05.2019 18:10
Вбочке 18 л томатного сока. хватит ли 5 -ти трехлитровых банок, чтобы разлить весь сок? как записать условие ?...
lyagaeva87 lyagaeva87  17.05.2019 18:10
Андрей наудачи выбирает трёхзначное число, найдите вероятность, что оно делится на 100, подробно...
alexxxay alexxxay  17.05.2019 18:10
Какие мероприятия по защите населения проводятся во время наводнения (обж 7 класс)...
dana085 dana085  17.05.2019 18:10
Поезд проехал 210 км со скоростью 70 км/ч. на остальной путь ему потребовалось при той же скорости на 4 часа больше. сколько всего км должен пройти поезд?...
dinadaybert dinadaybert  17.05.2019 18:10
Кто хорошо разбирается по татарскому языку. синонимы к словам азык эдэпле батыр былтыр гадел дөрес җиңел антонимы ко словам тиз ерак югары иртә килә эре киң усал юмарт надан калын...
sveta454 sveta454  17.05.2019 18:10
Ученые нашли две кладки яиц динозавров. в одной было 37 яиц, в другой - 30 яиц. общая масса первой кладки на 42 кг больше, чем масса второй. какова общая масса двух кладок?...
MARYA5478 MARYA5478  17.05.2019 18:10
На верстаті за 1 годину обробляли 7 детелей обробляли ,а після вдосконалення --9 деталий . на скільки деталей ? дайте условия и решение...
Colnkor Colnkor  17.05.2019 18:10
Длина оконного стекла прямоугольной формы равна 12 дм ширина 6дм найди площадь 14таких стекол...
mchervina mchervina  17.05.2019 18:10
Нужно решить 3 ! и желательно и краткую запись написать! 1. автомашина догнала мотоциклиста через 0,4 ч. скорость автомашины 70 км/ч, а скорость мотоциклиста 45км/ч. какое расстояние...
lsoft lsoft  17.05.2019 18:10
Есть кубики с ребрами 1 дм и 2 дм. нужно заполнить ими коробку со сторонами 3 дм, 5 дм и 8 дм так, чтобы не было пустого места и было использовано наименьшее количество кубиков. сколько...

Популярные вопросы