Математика: Вычислить площадь фигуры, ограниченной линиями y=8-x^2 и y=4

Вычислить площадь фигуры, ограниченной линиями y=8-x^2 и y=4

Ответы

nastusa098 18.07.2021 11:38

Сначала строим рисунок (см.). На нём сразу видны абсциссы точек пересечения, но для точности найдём их аналитически:

$8-x^2=4\\-x^2=-4\\x^2=4\\x= \pm 2$

Значит, мы находим интеграл на интервале [−2; 2].

Искомая площадь :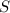

$S=\displaystyle \int \limits _{-2}^2(8-x^2-4) \, dx=\left(4x-\dfrac{x^3}{3}\right)\Bigg |^2_{-2}=\\=8-\dfrac{8}{3}-\left(-8+\dfrac{8}{3}\right)=16-2 \cdot \dfrac{8}{3}=16-\dfrac{16}{3}=\dfrac{32}{3}.$

Вычислить площадь фигуры, ограниченной линиями y=8-x^2 и y=4

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

dauren1mukumov 15.10.2019 20:29

Напишите что может показывать термометр по порядку: например 1. 3градуса тепла и т.д...

Staz134 15.10.2019 20:29

Реши линейное уравнение: -0,2g+11=15....

Каала 15.10.2019 20:30

При каких значениях х на [0; 2π) функция y=sinx+2 принимает наибольшее и наименьшее значение и чему оно равно...

SoloniyOgurets 15.10.2019 20:31

Решить контрольную. если не всю, то хоть сколько...

Даниад 15.10.2019 20:31

Какое число надо уменьшить в 18 раз, чтобы получить 5? увеличь 11 в 6 раз. найди частное чисел 48 и 4....

Danil24052002 15.10.2019 20:31

мистер фокс спрятал значок в одну из пяти шкатулок. затем написал четыре предложения: “значок в первой, второй или третьей шкатулке”,“значок в первой или пятой шкатулке”,“значок...

Zolotareva1981 15.10.2019 20:32

Велосипедист за 4 часа проехал 48 км а всадник за 3 часа км на сколько скорость велосипедиста больше скорости всадника ...

Dinkaakissa20 15.10.2019 20:32

Реши линейное уравнение: 7,5+9+(-0,94s)=13+7,5−1,04s....

kalmuratov70 15.10.2019 20:33

Сделать все номера мне не ханю...

Ilya333444 15.10.2019 20:33

Используй ровно шесть различных цифр и знаки финиш ский действий плюс минус умножить разделить получите число 2019 из цифр можно составлять число...

Вычислить площадь фигуры, ограниченной линиями y=8-x^2 и y=4

Популярные вопросы