Вычислить площадь фигуры, ограниченной линиями
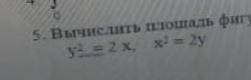
Другие вопросы по теме Математика
Популярные вопросы
- Железо составляет 90% сплава, остальное- никель. сколько кг железо и никнлч содержатся...
2 - Расстояние между пристанями a и b моторная лодка проплывёт против течения реки за...
3 - 1)вычаслите х в 5 степени +6 при х=-1 2)сравните значение выражений 3х+4 и 4х-2...
1 - За20 кг картофельная заплатили6 рубля. сколько картофеля можно купить на 9 рублей...
1 - Указать верну пропорцию: 6: 3=20: 10 4: 3=10: 15 5: 10=4: 4 12: 18=3: 2...
2 - Можно рассказать про какую-нибудь традицию? понятно и чтоб было не сильно много...
3 - Ручка стоит в 3 раза дороже тетради. сколько стоит тетрадь ,если стоимость ручки...
2 - Три реки дон, северский донец и сал протекают в городах семикаракорск, ростов, каменск....
1 - Как компилировать .cpp в .exe? в microsoft visual studio 2013...
1 - ответить на 3 вопроса. нужно. 1. легко ли дружить? 2. за что ты ценишь свою подругу?...
3
Пошаговое объяснение:
y² = 2x ⇒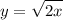
x² = 2y ⇒ y= x²/2
теперь рисуем графики, определяем фигуру и пределы интегрирования