Вычислить определенный интеграл
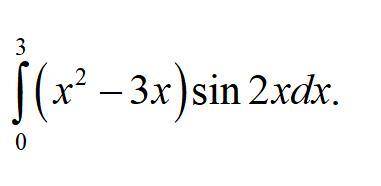
Другие вопросы по теме Математика
Популярные вопросы
- Придумайте предложения со словами биография, профессор, талант, коллекция,...
2 - Мальчик после разбега начинает скользить по льду со скоростью 8 м/с и через...
1 - Выпишите номера правильных утверждений: 1. общий облик растений - жизненная...
3 - 5пословиц поговорок на казахском языке на тему ана тiлi...
1 - Укажите слова с проверяемой безударной гласной в корнедогорать,мораль,монархия,седею,мозоль...
3 - Сделать фонетический разбор слова,пахнут...
1 - Из восьми членов нужно выбрать председателя казначея секретаря. скользкими...
1 - Три бригады сторителей должны посторить 2 одиннаковых дома. н а строительство...
3 - Укажите слова,которые с не пишутся слитно а)(не)ровная дорога б)трава (не)скошена...
3 - Сочинение на тему дорога таит в себе некую тайну величие...
1
Берем по частям: