Вычислить определенный интеграл
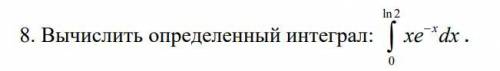
Другие вопросы по теме Математика
Популярные вопросы
- 525. выполните деление ответ на фото...
1 - Read and explain why do following words sound like: like, chick ,five ,lip, fine,...
2 - сделайте английский, это очень важно,...
1 - Подчеркните все верные продолжения высказывания ...
2 - Яке явище суспільного життя ілюструють зображення?...
1 - Звукоопис до слова подружці...
1 - Чуваки кто не в теме не спамьте ответы кому непонятно пишите в коментарии...
1 - 2 1/6 : (8 3/4 - 5 1/2) Можете отвечать развернута а не просто ответ желательно...
3 - Сакские племена объединяются в...
1 - Согласны ли вы со словами автора в Адвечным шляхам ( Извечным путём )? Актуально...
1
По частям: