Вычислить определенный интеграл
Другие вопросы по теме Математика
Популярные вопросы
- 50 . вычислить площадь фигуры ограниченной линиями. ...
2 - Написать рассказ о пальме от лица бразильца...
2 - Почему нельзя переливать 2 группу крови в третью...
2 - 108.спишите предложения ,объясните ,какой член предложения выражен...
1 - Разобрать слова по составу: свежость, лунными, сонным, лесом,...
3 - При недостатке кальция в организме назначают внутрь 10% раствор...
3 - Program gp; uses crt; var r: real; begin write( ввидите радиус...
3 - школа исследователя сравнение особенностей циклона и антициклона...
2 - Если (x0, y0) решение системы линейных уравнений {x+2y=-3 {3x+2y=5...
3 - 35 найдите точки экстремума функции...
2
ответ: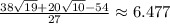
Пошаговое объяснение:
Найдем неопределенный интеграл:
Подставим значения: