вычислить объем тела образованного вращением фигуры ограниченной линиями вокруг оси ox. y=8+2x-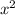 $x^{2}$ , y=2x+4 , y=0, x=0

Ответы

айрат36 18.05.2021 21:12

Пошаговое объяснение:

рисуеи графики, определяем фигуру, границы интегрирования

когда будем вертеть эту штуку вокруг оси ох, получим такую чашу с конусом внутри и выпуклыми боками.

$\displaystyle V=\pi \int\limits^2_{-2} {\bigg (-x^2+2x+8)^2} -(2x+4)^2\bigg )\, dx =$

$\displaystyle =\pi \int\limits^2_{-2} {(x^4-4x^3-16x^2-16x+48)} \, dx =$

$\displaystyle =\pi \bigg (\frac{x^5}{5} -x^4-16\frac{x^3}{3} +8x^2+48x\bigg ) \bigg |_{-2}^2=\frac{1792}{15} \pi$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

oilga03 08.08.2019 16:00

Россия111111111111 08.08.2019 16:00

BestPe 08.08.2019 16:00

Вчем сходства и в в чем отличия звезд от планет?...

rudneva04 08.08.2019 16:00

Слава200109 08.08.2019 16:00

adamannik 08.08.2019 16:00

Найдите значение выражения a^2-9b^2/3ab: (1/3b-1/a)...

kery99 08.08.2019 16:00

Slysly 08.08.2019 16:00

8300: 10-30 36*1000+20. 200: (310-300): 5. 400: (460-360)*4. 61000-1. 49099+1...

gulmamedovaxayald 08.08.2019 16:00

theartik1 08.08.2019 16:00

У^2-6у+5 корни кавдратного трехчлена...

вычислить объем тела образованного вращением фигуры ограниченной линиями вокруг оси ox. y=8+2x- , y=2x+4 , y=0, x=0