Вычислить криволинейный интеграл: 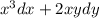 от точки А(0;0) до точки В(1;1) по линии
от точки А(0;0) до точки В(1;1) по линии ![\sqrt[4]{x}](/tpl/images/4742/2854/846fb.png)
Другие вопросы по теме Математика
Популярные вопросы
- Укажи основную тему творчества сказителей и жырау XVIII века. о...
2 - На сколько периодов делится древняя история человечества?...
2 - 53 - бет , 5 - тапсырма , 7 сөйлем , сөйлемде қолданған неологизм...
1 - А) Составьте схемы предложений 1-3. 1) Марс ближайший сосед нашей...
2 - Элементы понятия биотехнология...
2 - Көшпелілер кто таки можете ответить на каз яз...
1 - 2. Плотность редкого металла осмия равна КГ22 600Что означает это...
1 - Мәтінді оқы авторына сілтеме жасаңдар оны айғақтайтын тілдік деректерді...
1 - Умножение и деление рациональных дробей Возведение рациональной...
2 - особенности строения Пищеварительной, дыхательной, выделительной,...
2
Вычисляем криволинейный интеграл 2 рода , заменяя у и dy выражениями через переменную х .