Популярные вопросы
- Слово какой части речи и какой формы может быть задуманное, если...
3 - Соседний гомолог циклобутана 1)пропан 2)метилпропан 3)циклопропан...
1 - План конспект на тему мировой океан и его части 5 класс...
3 - Вынесите за скобки общий множитель b(y-z)+c(z-y)...
2 - Описание внешности тараса бульбы описание внешности бирюка...
2 - 1)какая чать россии-европейская или азиатская-наиболее обеспечены...
3 - 624 : 7 9163: 5 249: 6 1224: 4 64: 16 165: 52...
1 - Выберите верное утверждение. а. живые организмы имеют черты при...
3 - Обществознание 6 класс как составить словарик таких без слов средств...
3 - Решите уравнение : 1) 1376 : (34-x)=86; 2) 8680 : (x+219) =16;...
3
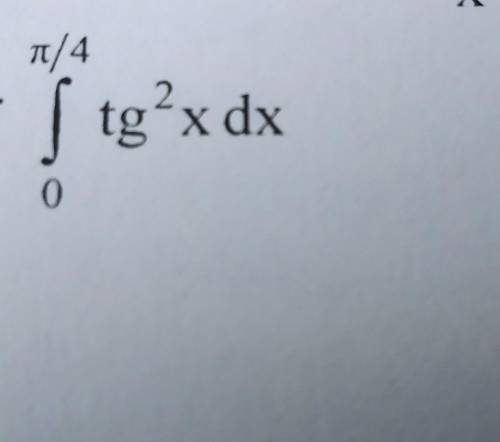
Пошаговое объяснение: