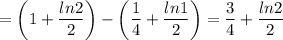Вычислить длину дуги кривой
Другие вопросы по теме Математика
Популярные вопросы
- .Ich lebe (1) in Nishyn. Das ist eine(2) Stadt. Sie ist über 1000 ......
1 - решить задачу решить задачу...
1 - Неправильно вжито прийменник:1) досягнув завдяки наполегливості2) переміг...
1 - Y={x^2,если x≤1, 1/x, если класс...
3 - Прямая, перпендикулярная к каким-нибудь двум прямым, лежащим в плоскости,...
3 - Знайти область визначення функції: y=6x²+7х-9...
1 - хоть с чем-нибудь хоть с чем-нибудь хоть с чем-нибудь...
3 - РЕШИТЬ ТЕСТ ДАЮ 40 Б. Во Какое из приведенных утверждений является логическим...
1 - 1. як розміщені максимуми відносно центрального і чому? 2. чому нульовий...
3 - Спишите предложение с однородными членами. Поставьте необходимый знак...
3
Пошаговое объяснение:
Тогда длина кривой равна![l=\int\limits_1^2\sqrt{1+y'^2}dx=\\ =\left[1+\left(\dfrac{x}{2}-\dfrac{1}{2x}\right)^2=1+\dfrac{x^2}{4}-\dfrac{1}{2}+\dfrac{1}{4x^2}=\dfrac{x^2}{4}+\dfrac{1}{2}+\dfrac{1}{4x^2}=\left(\dfrac{x}{2}+\dfrac{1}{2x}\right)^2\right]=\\ =\int\limits_1^2\left|\dfrac{x}{2}+\dfrac{1}{2x}\right|dx=\int\limits_1^2\left(\dfrac{x}{2}+\dfrac{1}{2x}\right)dx=\left(\dfrac{x^2}{4}+\dfrac{lnx}{2}\right)\Big|\limits_1^2=\left(\dfrac{2^2}{4}+\dfrac{ln2}{2}\right)-\left(\dfrac{1^2}{4}+\dfrac{ln1}{2}\right)=\\](/tpl/images/2004/2013/86038.png)