Вычислить: √3)/2)+arcsin(1/2)+arcctg√3 решите уравнения: 1.√(x-3)=x-5 2. (√x)+3(корень четвертой степени из x)-10=0
Ответы
Arccos(-(√3)/2)+arcsin(1/2)+arcctg√3=π-arccos(√3/2)+arcsin(1/2)+arcctg√3=π-π/6+π/6+π/3=2π/3
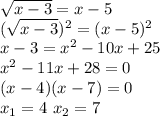
![\sqrt{x} +3 \sqrt[4]{x} -10=0 \\ y= \sqrt[4]{x} \\ y^2+3y-10=0 \\ (y+5)(y-2)=0 \\ y_1=2 \ y_2=5 \\ \sqrt[4]{x} =2 \ \sqrt[4]{x} =-5 \\ x=2^4 \\ x=16](/tpl/images/0770/3207/678f6.png)
ПОКАЗАТЬ ОТВЕТЫ
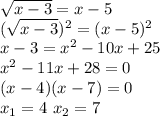
![\sqrt{x} +3 \sqrt[4]{x} -10=0 \\ y= \sqrt[4]{x} \\ y^2+3y-10=0 \\ (y+5)(y-2)=0 \\ y_1=2 \ y_2=5 \\ \sqrt[4]{x} =2 \ \sqrt[4]{x} =-5 \\ x=2^4 \\ x=16](/tpl/images/0770/3207/678f6.png)
Другие вопросы по теме Математика
Популярные вопросы
- Запишите название любого объекта (города, населённого пункта, реки или который...
3 - Вопрос по произведению уроки французского жизнь героя вдали от дома, какие...
3 - Какой вклад внёс токио в стабилизацию внутреннего положения казахского ханства...
1 - Элементы с которыми хлор образует ионную связь...
3 - Высота правильной четырехугольной призмы равна 8√3 , а сторона основания...
1 - На 1 корабле-134 т груза на ? т груза больше на 2 корабле-? ,в 5 раз больше...
3 - Эссе что значит для меня семья зделать мне осталось мало время до...
3 - They last year visit england didint...
3 - Пересказ произведения конь с розовой гривой от лица бабушки (катерины петровны)...
2 - Начерти прямоугольник, длина которого 9 см, а ширина в 3 раза меньше длины....
3