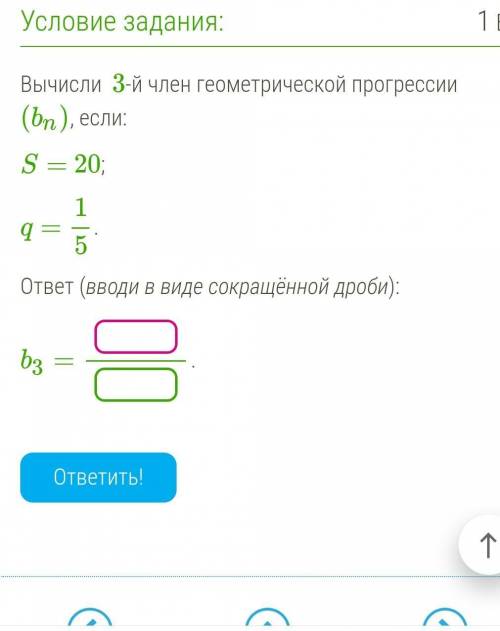
Вычисли  3-й член геометрической прогрессии (bn), если: S= 20;
q= 1/5.
ответ (вводи в виде сокращённой дроби): b3=.

Для вычисления 3-го члена геометрической прогрессии (b3) с данными значениями S и q, нам необходимы следующие шаги:

1. Зная сумму первых n членов геометрической прогрессии (S) и знаменатель прогрессии (q), мы можем использовать формулу для суммы n членов геометрической прогрессии:
S = a * (1 - q^n) / (1 - q),

где a - первый член прогрессии.

2. В данном случае, нам дано, что S = 20, поэтому мы можем записать это в уравнении:
20 = a * (1 - (1/5)^n) / (1 - 1/5).

3. Чтобы упростить уравнение, мы можем избавиться от дробей в знаменателе, умножив обе стороны уравнения на 5:
100 = 5a * (1 - (1/5)^n).

4. Теперь мы можем заменить b3 вместо a (поскольку нам нужно вычислить 3-й член геометрической прогрессии) и записать:
100 = 5b3 * (1 - (1/5)^3).

5. Теперь мы можем вычислить (1/5)^3, которое равно 1/125:
100 = 5b3 * (1 - 1/125).

6. Упростив уравнение, мы получаем:
100 = 5b3 * (124/125).

7. Чтобы выразить b3, разделим обе стороны на 5 * (124/125):
b3 = 100 / (5 * (124/125)).

8. Для удобства дальнейших вычислений, домножим числитель и знаменатель на 25:
b3 = (100 * 25) / (5 * 124).

9. Затем произведем умножение в числителе:
b3 = 2500 / (5 * 124).

10. И, наконец, умножим в знаменателе:
b3 = 2500 / 620.

Итак, значение 3-го члена геометрической прогрессии (b3) равно 4/31. Ответ в виде сокращенной дроби: b3 = 4/31.