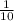Вурне имеется пять шаров с номерами от 1 до 5. наудачу по одному извлекают три шара без возвращения. найти вероятности следующих событий: а) последовательно появятся шары с номерами 1, 4, 5; б) извлеченные шары будут иметь номера i, 4, 5 независимо от того, в какой последовательности они появились.
Другие вопросы по теме Математика
Популярные вопросы
- На каком расстоянии от точечного заряда 8 нкл потенциал электрического...
2 - Нет такой книги, из которой человек не мог бы научится кое- чему хорошему....
3 - А3: какие частицы являются носителями тока в металлических проводниках?...
2 - Как узнать, намагничены или нет лезвия ножниц?...
1 - 1. составьте структурные формулы: а) метилэтиламина б) 5-аминовалериановой...
1 - Дано 5 чисел. определить сколько среди них положительных. составьте,...
3 - Втреугольнике абс с=90,в=60,св=6 см.чему равна сторона ав? надо решение...
2 - Скласти діалог на тему журналіст брав інтервю у знаменитості...
1 - Как можно объяснить слова деда лариона : этот заяц , можно ,сказать...
2 - Запишите в ответе номера верных неравенств 1) (2-b)(b+2)=b^2-4 2)...
1
а) Всего в урне 5 шаров. Шар с номером 1 единственный.
Значит вероятность извлечения шара под номером 1 будет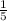
Теперь в урне 4 шара. Шар под номером 4 единственный. Вероятность извлечения шара под номером 4: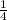
В урне осталось 3 шара, из которых один под номером 5. Вероятность извлечения шара под номером 5: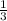
Перемножим полученные вероятности и узнаем вероятность наступления события "Последовательно появятся шары с номерами 1, 4, 5"
ответ: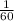
б) Всего в урне 5 шаров. Нужно вытащить шар под номером 1, или 4, или 5, т.е. благоприятных исходов 3.
Вероятность вытащить шар с номером 1, или 4, или 5:
В урне осталось 4 шара. Благоприятных же исходов теперь 2, т.к. один нужный шар уже убрали.
Вероятность вытащить шар с нужным номером: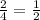
В урне осталось 3 шара. Благоприятных исходов осталось 1, т.к. два шара с нужными номерами убрали.
Вероятность вытащить шар с нужным номером: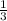
Теперь нужно перемножить найденные вероятности, т.к. мы находим вероятность одновременного наступления независимых событий.
ответ: