Всем привет, очень объясните как складывать, умножать и вычитать дроби с разными знаменателями, а ещё и смешаннымы числами, ВПР скоро(((​

Пошаговое объяснение:

Смотри:

1) Множить очень легко

Числительное множишь на числительное, а знаменательное на знаменательное:

2)если складывать и вычитать, то приводишь к общему знаменателю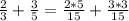

Я зделал так, что-бы знаменательные были одинаковыми(нужно до числительного и знаменателя обоих домножить такое число, чтобы знаменатели обеих чисел были одинаковые). С вычитанием тоже, только вычитать числительные, если знаменатели уравнены

3) тут я не знаю как объяснить. Сорян

сложение и вычитание.

здесь нужно работать по одному принципу, просто приводишь дроби к общему знаменателю, к наименьшему общему кратному. при приведении дробей к общему знаменателю тебе нужно умножать и числитель, и знаменатель, это важно.

например 2/3 + 3/6

в нашем случае знаменатели - 3 и 6, шесть является наименьшим общим кратным, поэтому, вторую дробь мы не трогаем, а домнодаем до 6 первую, то есть умножаем на 2. 2/3 *2 (умножаем обе части дроби) = 4/6, выходит 4/6 + 3/6 = 7/6 здесь ещё можно будет выделить целую часть (если числитель больше знаменателя, смотрим сколько знаменателей есть в числителе, ну или можно просто разделить числитель на знаменатель) и получаем 1 1/6

бывают случаи, когда знаменатель одной дроби не является наименьшим общим кратным, тогда в этом случае мы домножаем обе дроби, например 2/3 + 2/4

находим наименьшее общее кратное, умножая больший знаменатель (4*2=8 8 на 3 не делится, значит не подходит, 4*3=12 12 на 3 делится, значит мы нашли наше наименьшее общее кратное), теперь домножаем оба знаменателя до 12 2/3 домножаем на 4, получаем 8/12, 2/4 домножаем на 3, получаем 6/12

в итоге 8/12 + 6/12 = 14/12 здесь тоже можно выделить целую часть и получаем 1 2/12, сокращаем — 1 1/6

с вычитанием ситуация идентичная

умножение

здесь просто перемножают числитель на числитель и знаменатель на знаменатель

например 3/4 * 5/6 = 15/24

чем больше тренироваться, тем получаться будет лучше

деление

при делении повторяется принцип умножения

например, нам надо 3/5 : 6/4

ВСЕГДА ПЕРЕВОРАЧИВАЕМ вторую дробь и ЗАМЕНЯЕМ деление на умножение

получаем 3/5 * 4/6 = (повторяем те же действия, что и при умножении) 12/30

смешанные дроби

все действия со смешанным дробями начинаются с того, что мы делаем их них неправильную дробь (действие, обратное выделению целой части, то есть то, что мы делали на примере сложении и вычитании)

например, нам нужно 1 2/3 + 3 3/4

чтобы превратит смешанную дробь в неправильную нужно целую часть умножить на знаменатель и прибавить к этому числитель, то есть (на примере дроби выше) 1 умножаем на 3 и прибавляем к этому два, получается 5 - это ЧИСЛИТЕЛЬ нашей неправильной дроби, ЗНАМЕНАТЕЛЬ пишем ПРЕЖНИЙ, то есть получается 5/3

со второй дробью то же самое: 3 умножаем на четыре и прибавляем 3, выходит 15 в числителе и 4 в знаменателе 15/4

возвращаемся к примеру 5/3 + 15/4 (общий знаменатель 12, как и в случае, домножаем дроби) 5/3 на 4 и 15/4 на 3, получается 20/12 + 45/12 = 65/12 = (выделяем целую часть) 5 5/12

а так все те же самые махинации, что и с обычными дробями.