Впартии из 12 деталей имеется 9 стандартных. найдите вероятность того, что среди семи взятых наугад деталей 6 стандартных? распишите решение подробней

Ответы

Ztduvuycc 19.07.2020 09:15

В партии 12 - 9 = 3 деталей бракованных

Общее число возможных элементарных исходов для данных испытаний равно числу которыми можно извлечь 7 детали из 12:

$C^7_{12}=\dfrac{12!}{7!5!}=792$

Подсчитаем число исходов, благоприятствующих данному событию:

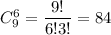одну деталь среди 3 бракованных можно выбрать количество которых равно: C^1_3=3 , а шесть деталей среди 9 стандартных можно выбрать $C^6_9=\dfrac{9!}{6!3!}=84$ . По правилу произведения, всего благоприятных исходов: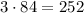 $3\cdot84=252$

Искомая вероятность: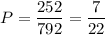 $P=\dfrac{252}{792}=\dfrac{7}{22}$

ПОКАЗАТЬ ОТВЕТЫ

хорошистка553 19.07.2020 09:15

Выбрать из 12 деталей 7 можно с выбрать из 9 стандартных деталей 6 стандартных можно с и одну нестандартную из (12-9) трех нестандартных с т.е. выбрать 7 деталей, среди которых 6 стандартных, можно с Искомую вероятность находим с формулы классического определения вероятности m/n=

(3*9!/(6!*3!))/(12!/(7!*5!))=(3*9!*7!*5!)/(6!*3!*12!)=7/(2*11)=7/22

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика