Возвращаясь с работы, гномы шли цепочкой. Шедший восьмым гном Нолик заметил погреб. Гномы зашли в него и увидели одинаковые бочки полные эля. Они выпили 10 бочек и отправились спать. Причем все выпили поровну. Пока остальные гномы спали, семеро решили вернуться и допить эль. Каждый из них выпил ровно половину выпитого им ранее количества, и эль закончился. Сколько бочек эля было в погребе первоначально?
ОЧЕНЬ заранее

Пусть всего было х+7 гномов. Тогда когда 7 гномов допивали эль, х гномов спали.

В первый раз х+7 гномов выпили 10 бочек. То есть каждый гном выпил часть бочки.

А во второй раз 7 гномов выпили часть бочки каждый. И эль закончился.

Всего было выпито бочек:

Количество бочек очевидным образом, является натуральным числом. 35=5·7 ⇒ x+7=5 или x+7=7 или x+7=35

х так же натуральное число, тогда подходит только уравнение x+7=35 ⇔ x=28

Тогда всего было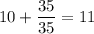 бочек.

ответ: 11.