Вопрос Найдите все значения nεN, при которых значение функции
f(n) = 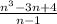
является натуральным числом.
Другие вопросы по теме Математика
Популярные вопросы
- Variant 1 1. Choose the correct word from the box to match the definitions....
3 - Дайте полное описание химического элемента по названию и количеству...
3 - Складно сурядне речення з тире, крапка з комою, без коми (по 2 приклади)...
2 - Брусок, лежащий на горизонтальном столе, при сообщении скорости 2...
2 - Напишите мини информацию про қазақ...
2 - Сұрақтарға жауап бер 4 класс 121 бет 5 тапсырма 1)Абай Қунанбайұлы-кім?...
3 - У якому рядку використано епітет А) там русский духВ) З ягою ступа...
3 - Составьте предложения с глаголами из скобок, используя подходящие...
2 - В школьну столовую привезли 120 кг картофеля. В первый день израсходовали...
2 - Дайте відповідь на запитання: 1) З яких частинок складається кухонна...
3
2 делится на (n-1):