вообще ничего не понимаю...
Найти числовой ряд на сходимость
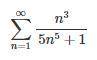
Другие вопросы по теме Математика
Популярные вопросы
- ответить на вопросы - по одному предложению:1/объясните, почему кочеваниеосуществлялось...
2 - решить годовую нужно закрывать >...
3 - Чому Конрад ставить Берті так багато запитань? Чи легко їй відповідати?Як порозумілися...
3 - , решите задачку по химии При выпаривании 150 г 10% раствора NaCl в остатке получили...
3 - Определить: 1. Индекс покупательной рубля. 2. Индекс реальных располагаемых денежных...
3 - Составьте общий вопрос и специальный вопрос 1.The transistor occupied an important...
2 - 3. Writing/ 4 points. Complete the sentences using Present Continuous. 1. We (have)...
1 - Написання формального есе на тему Мозаїка української душі (миролюбність, сміливість,...
3 - 1.If people do physical activities at a regular basis, they strengthen their muscles...
3 - 124 бет, 5-тапсырма. Мәтінде сипатталған халқымыздың бастан кешкен ең ауыр күндері...
2
Відповідь:
ряд збігається
Покрокове пояснення:
Знайдемо границю n+1 члена ряду до n-го при n→бескінечності
(n+1)^3/(5(n+1)^5+1) : n^3/(5n^5+1) = n^3(1+1/n)^3 / (n^5(5(1+1/n)^5+1/(n^5) × n^5(5+1/n)/(n^3)=
=(1+1/n)^3 / ((5(1+1/n)^5+1/(n^5) × (5+1/n)/1
При n→бесконечности а_(n+1)/a_n→1/(5^5)×5/1=1/(5^4)=
=1/625=0,0016<1. то ряд збігається
Пошаговое объяснение:
используем признак сравнения
рассмотрим предел общего члена
упростим его
тогда исходный ряд можно представить в виде
а это обобщенный гармонический ряд с α > 1
тогда и исходный ряд сходится.