Вокружности проведены две хорды. расстояние от центра окружности до первой хорды равно 60, а до второй 52. найдите длину второй хорды, если длина первой хорды равна 50.

Ответы

Наркодилер 26.08.2020 19:54

ответ:

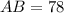AB = 78 ед.

Пошаговое объяснение:

Обозначим окружность с центром в точке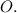

OR = 60 ед.

OS = 52 ед.

CD = 50 ед.

OM, ON, OB, OD - радиусы данной окружности.

===========================================================

Если радиус окружности перпендикулярен к хорде окружности, то он делит хорду пополам.

$ON \perp CD$ , так как $OR \perp CD$ (расстояние от точки до прямой - это перпендикуляр).

$\Rightarrow CR = RD = CD : 2 = 50 : 2 = 25$ ед.

Рассмотрим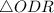 $\triangle ODR$ :

$\triangle ODR$ - прямоугольный, так как $OR \perp CD$ .

Найдём радиус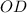 по теореме Пифагора:

$OD^{2} = OR^{2} + RD^{2} = 60^{2} + 25^{2} = 4225$

$OD = \sqrt{4225} = 65$ ед.

===========================================================

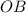Так как и 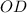- радиусы окружности 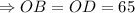$\Rightarrow OB = OD = 65$ ед.

Рассмотрим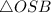 $\triangle OSB$ :

$\triangle OSB$ - прямоугольный, так как $OS \perp AB$ (расстояние от точки до прямой - это перпендикуляр).

Найдём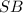 по теореме Пифагора:

$SB^{2} = OB^{2} - OS^{2} = 65^{2} - 52^{2} = 1521$

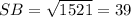$SB = \sqrt{1521} = 39$ ед.

Если радиус окружности перпендикулярен к хорде окружности, то он делит хорду пополам.

$OM \perp AB \Rightarrow AB = SB \cdot 2 = 39 \cdot 2 = 78$ ед.

Вокружности проведены две хорды. расстояние от центра окружности до первой хорды равно 60, а до втор

ПОКАЗАТЬ ОТВЕТЫ

inchinusaozkhxs 26.08.2020 19:54

78 (единиц)

Пошаговое объяснение:

Дано (см. рисунок):

Окружность радиуса R

AB=50 – длина первой хорды

OM=60 – расстояние от центра O окружности до хорды AB

ON=52 – расстояние от центра O окружности до хорды CD

Найти: x=CD – длину второй хорды

Решение.

Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 60. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 52.

Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:

1) длина MB=50:2=25 и длина ND=x:2;

2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.

Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:

R² = OM²+MB² = 60²+25² = 3600+625 = 4225 = 65² или R=65.

Применим теорему Пифагора к прямоугольному треугольнику OCD:

R² = ON²+ND² = 52²+(x:2)² или

(x:2)² = R²–52² = 65²–52² = 4225–2704 = 1521 = 39² или

x:2 = 39.

Отсюда CD=x=39·2 = 78 (единиц).