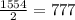1. Математика
  2. Водном сосуде 1554 литра

Водном сосуде 1554 литра воды,другой пустой.из первого сосуда переливают ½ воды во второй, затем из второго переливают ⅓ воды в первый, затем из первого переливают ¼ во второй и так далее. сколько литров воды будет в первом сосуде после 2019-го переливания.

рай34 рай34    3   14.12.2019 21:28    1

Ответы
anuta136 anuta136  11.09.2020 16:29

777 литра

Пошаговое объяснение:

Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.

1-переливание. Переливаем с 1-сосуда во 2-сосуд:

1-сосуд: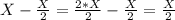 X-\frac{X}{2} = \frac{2*X}{2}-\frac{X}{2} =\frac{X}{2}

2-сосуд: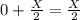 0+\frac{X}{2} = \frac{X}{2}

Объем воды в обоих сосудах в сумме дают Х литр!

2-переливание. Переливаем со 2-сосуда в 1-сосуд:

1-сосуд: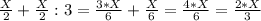  \frac{X}{2}+\frac{X}{2}:3=\frac{3*X}{6}+\frac{X}{6}=\frac{4*X}{6}=\frac{2*X}{3}

2-сосуд: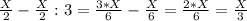 \frac{X}{2}-\frac{X}{2}:3=\frac{3*X}{6}-\frac{X}{6}=\frac{2*X}{6}=\frac{X}{3}

Объем воды в обоих сосудах в сумме дают Х литр!

3-переливание. Переливаем с 1-сосуда во 2-сосуд:

1-сосуд: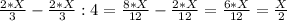 \frac{2*X}{3}-\frac{2*X}{3}:4=\frac{8*X}{12}-\frac{2*X}{12}=\frac{6*X}{12}=\frac{X}{2}

Так как, объем воды в обоих сосудах в сумме дают Х литр, то

2-сосуд: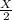 \frac{X}{2}

Теперь покажем, что в нечётных числах переливания всегда

1-сосуд: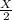 \frac{X}{2}

2-сосуд: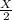 \frac{X}{2}

Пусть n=2·k+1.

n-переливание. Переливаем с 1-сосуда во 2-сосуд:

1-сосуд: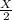 \frac{X}{2}

2-сосуд: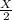 \frac{X}{2}

(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:

1-сосуд: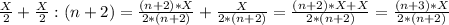 \frac{X}{2}+\frac{X}{2}:(n+2)=\frac{(n+2)*X}{2*(n+2)}+\frac{X}{2*(n+2)}=\frac{(n+2)*X+X}{2*(n+2)}=\frac{(n+3)*X}{2*(n+2)}

2-сосуд: \frac{X}{2}-\frac{X}{2}:(n+2)=\frac{X*(n+2)}{2*(n+2)}-\frac{X}{2*(n+2)}=\frac{X*(n+1)}{2*(n+2)}

(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:

1-сосуд: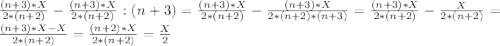 \frac{(n+3)*X}{2*(n+2)}-\frac{(n+3)*X}{2*(n+2)}:(n+3)=\frac{(n+3)*X}{2*(n+2)}-\frac{(n+3)*X}{2*(n+2)*(n+3)}=\frac{(n+3)*X}{2*(n+2)}-\frac{X}{2*(n+2)}=\frac{(n+3)*X-X}{2*(n+2)}=\frac{(n+2)*X}{2*(n+2)}=\frac{X}{2}

Так как, объем воды в обоих сосудах в сумме дают Х литр, то

2-сосуд: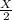 \frac{X}{2}

что требовалось показать.

Отсюда, 2019 - нечётное и X=1554 литра, тогда

1-сосуд: \frac{1554}{2}=777

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
VovaMel2017 VovaMel2017  06.05.2020 10:53
СОР Система подстановки 10х-4у-30=0 4х-2у=14...
mmatomagomedova mmatomagomedova  06.05.2020 10:53
1) Площадь кватрада 36 см.кв какой длины в см могут быть стороны прямоугольников с токойже площадью как у кватрада? найди периметр каждого из них2) Найди длину стороны равностороного...
polosa48rus polosa48rus  06.05.2020 10:53
Представлены градусные величины углов. Выберите прямой угол. Варианты ответов 197° 89° 180° 90°...
виктория123600 виктория123600  06.05.2020 10:53
Есептин шешуин арипти орнек туринде жаз d=12 к=13 m=21 деп алып орнектин манин тап...
Jfigh Jfigh  06.05.2020 10:53
CРОЧНОООООО 2cos^a-2sin^a-cos2a а-альфа...
Fluttershy0 Fluttershy0  06.05.2020 10:53
Розв яжіть рівняння 8 клас​...
katysha087 katysha087  06.05.2020 10:53
Как раситавить дроби от меншого до бильшого 5.6 1.2 0.3 1.1 0.1...
Dinadiamond Dinadiamond  06.05.2020 10:53
Решите уравнение sin^2 (x/2) +8cosx/2-7=0...
bur5645 bur5645  06.05.2020 10:52
ТЕЗ КЕРЕК МАҒАН Дариғаның қызыл және жасыл жейделері, көк және қара белдемшелері,сұр ,қоныр және ақ туфлилері бар.Дариға барлық жейделерін,белдемшелерін және туфлилерін ауыстырып...
8603184005291 8603184005291  06.05.2020 10:52
на сколько команд могут разделиться 12 мальчиков и 6 девочек?? ответ: на 1, ..., ..., или ... команд....

Популярные вопросы