Вначале учебного года студент купил x книг общей стоимостью 8. через несколько дней он купил еще 5 книг еще за 25000. он обнаружил, что вторая покупка снизила общую среднюю стоимость книги на 1000 . сколько всего книг он купил?
Другие вопросы по теме Математика
Популярные вопросы
- Автотуристы проехали 240км, проезжая 80км в час, а потом -420км, проезжая...
2 - Произведение чисел 15 и а .записать в виде буквенного выражения...
3 - 10 пословиц и поговорок используя книгу в.даля пословицы и поговорки народа...
1 - Охарактеризуйте успехи медицины на рубеже веков в чем заключались причины...
3 - Названия лесных цветов в начале осени...
2 - Какие живые организмы живут внутри человека...
1 - Записать и прочитать по порядку число,которое содержит. 5д. 0 ед. 1д....
1 - За две недели бригада собрала 113тонны картофеля из них за первую неделю...
1 - Как обьяснить значение слов машет-,трясет-потряхивает,гдядит-поглядывает...
3 - Слова крепкий сравнительной степени...
2
Средняя стоимость книг перед второй покупкой равна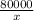
Средняя стоимость книг после второй покупки равна
Тогда по условию задачи получаем, что
По условию задачи x ≠ -5; 0, поэтому можем домножить обе части на x(x+5)
Корень x = -40 не удовлетворяет смыслу задачи. Значит, в первый раз он купил 10 книг. Учитывая книги, которые он купил потом, получаем ответ 15.
ответ: 15
15 книг
80000/x-105000/(x+5)=1000
(80000/x-105000/(x+5))*x=1000*x
25000*(16-x)/(x+5)=1000x
25000*(16-x)/(x+5)*(x+5)=1000x*(x+5)
400000-25000x=1000x²+5000x
-1000x²-30000x+400000=0
D=-30000²-4*(-1000)*400000=2500000000
x1=(√2500000000-(-30000))/(2*(-1000))=-40
x2=(-√2500000000-(-30000))/(2*(-1000))=10
10+5=15