Визначити координати фокусів, довжину осей та ексцентриситет гіперболи

Ответы

лёванчик228 06.07.2022 06:40

координаты фокусов: $\displaystyle \boldsymbol { F_1(-\sqrt{61} ;0)\qquad F_2(\sqrt{61} ;0)}$

длина осей : действительная ось 12; мнимая ось 10

эксцентриситет: $\displaystyle \boldsymbol {\varepsilon=\frac{\sqrt{61} }{6}}$

Пошаговое объяснение:

Каноническое уравнение гиперболы имеет вид

$\displaystyle \frac{x^2}{a^2} -\frac{y^2}{b^2} =1$

Приведем наше уравнение к каноническому виду.

900 переносим в правую часть и одновременно делим все части уравнения на 900.

$\displaystyle \frac{25x^2}{900} -\frac{36y^2}{900} =1frac{x^2}{6^2} -\frac{y^2}{5^2} =1$

Таким образом, мы получили каноническое уравнение гииперболы с центром в точке С(0; 0).

а = 6; b = 5

Действительная ось 2а = 12.

Мнимая ось 2b = 10

Расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: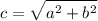 $\displaystyle c=\sqrt{a^2+b^2}$ .

Фокусы имеют координаты F₁ (-c; 0) ; F₂(c; 0).

Найдем фокусы нашей гиперболы.

$\displaystyle c=\sqrt{6^2+5^2}=\sqrt{36+25} =\sqrt{61} F_1(-\sqrt{61} ;0)\qquad F_2(\sqrt{61} ;0)$

Эксцентриситетом гиперболы это отношение

$\displaystyle \varepsilon=\frac{c}{a} =\frac{\sqrt{61} }{6}$

#SPJ1

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

julyyushchenko 16.10.2020 02:25

likeaboss2005 16.10.2020 04:05

MaxXXL2003 16.10.2020 01:48

Valeria13092004 16.10.2020 02:29

Запишити первые пять чисел кратные числу восем...

DellXT 16.10.2020 02:28

амина74726 16.10.2020 02:29

Sandra2516 16.10.2020 01:45

Координаталық түзуді қолданып, 9/6-25/10= 9-25/6+10...

Veronika509 16.10.2020 01:39

123ЭщКеРе123 16.10.2020 01:49

hrsalesaudit 16.10.2020 01:49