Висота правильної трикутної піраміди 15 см, а апофема піраміди - 17 см. знайти площу бічної поверхні. высота правильной треугольной пирамиды 15 см, а апофема пирамиды - 17 см. найти площадь боковой поверхности.

Дано : MABC - правильная пирамида. h = MO = 15 см - высота пирамиды. L = MN = 17 см  -  апофема.

Площадь боковой поверхности пирамиды равна произведению полупериметра основания на апофему :   S = pL

ΔMON - прямоугольный. Теорема Пифагора

ON² = MN² - MO² = 17² - 15² = (17-15)(17+15)=2·32 = 64 = 8²

ON = 8 см

Высота правильной пирамиды опускается в центр окружности, вписанной в равносторонний треугольник основания    ⇒    

r = ON = 8 см    и         ⇒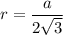

AB = CB = AC = a =  r · 2√3 = 8 · 2√3 = 16 √3 см

Площадь боковой поверхности пирамиды

см²

ответ :   408√3 см²